The didactic proposal Cell phones presented here is a contribution to the LOSSTT-IN-MATH project. It consists of a comparison of different tariff plans available for mobile phone calls. The subject has been chosen, because it is a major part of pupils´ every day life and because it is a rather complicated subject with many variables. In treating this, the competences of problem treating and modelling can be developed. In the proposals the tariff plans will be looked at through mathematics notions. The proposal was piloted by the following partners: Skårup Seminarium, University of Pisa and IUFM of Paris. For the first two partners the following scheme was contained in the proposal: Introduction for teacher trainees. In groups teacher trainees are discussing how to make the best lesson plan for pupils. A lesson plan is made. Teacher trainees are piloting the proposal in school.

Problem solving with brochures or commercials
The following unit is a part of LOSSTT-IN-MATH project piloted in Skårup Seminarium in the third year of teacher training in mathematics.
The teacher education takes four years and the teacher trainees are authorized to teach at primary and lower secondary schools.
Mathematics is a part of all four years, within the same team and normally with the same teacher trainer. Each week the teacher trainees are offered about five hour in this subject.
It is important that the pupils can manoeuvre in their daily life. There will be a lot of areas where mathematics is the only subject that can contribute to this. The pupils are bombed with commercials concerning mobile phones and they often use a lot of money on these. This subject really affects the pupils’ daily life and is very essential for them. At this age (13–14 years) they often administer shopping and payment themselves. Ann Tariff plan for mobile phones contains a lot of variables, which makes it very difficult for most people to determine what will be the best buy for their own needs. That is the reason why the didactic proposal “mobile phones” was chosen for the project. The teacher training students are asked to prepare a plan about this problem to be carried out in a lesson with pupils in the seventh class. The pupils should be provided with the necessary data, which are usually contained in a commercial. Looking at linear functions would be the most obvious thing to do. But the class has not worked on the notion of function and then the most obvious thing is to work on the notion of variable, as we have too little time to introduce the pupils to the notion of linear function.
The plan of the piloting in Skårup is shown in the following table:
|
Main persons involved |
Chronology |
Description |
|
Teacher trainer |
|
The teacher trainees are sent an introduction via e-mail. |
|
Teacher trainees |
1hr |
One teacher trainee has prepared an introduction, based on the information from the Internet. He informs the other trainees about prices concerning mobile phones. |
|
Teacher trainees in groups |
1hr |
The teacher trainees work in groups to plan the lesson with the pupils. |
|
Teacher trainees |
2hrs |
The whole team discusses how to make the lesson including the conditions for the lesson with the pupils |
|
Pupils and six teacher trainees |
1hr |
The lesson at school |
|
Teacher trainer and teacher trainees |
1hr |
Evaluation |
Table 1. Piloting plan
Number of trainers: 1 (a teacher at Skårup Seminarium)
Number of trainees: 25
Number of classes involved in the piloting: 1 (7th class)
Number and age of pupils: 20 pupils aged 13-14
Number of adults in each classroom during the lessons: 5 trainees (present for the first time in the classroom) the teacher and the teacher trainer.
For trainers:
· Providing information
· Helping the teacher trainees from theory to practice
· Evaluating
For trainees:
· To treat problem solving as a part of mathematics and under that to involve daily situations in mathematics education.
· To understand and use expressions, which include variables
· To discuss and develop a lesson plan
· To implement the lesson plan
For pupils:
· To treat problem solving as a part of mathematics
· To handle daily situations in their mathematics education
· To work on the notion of variable
· To manoeuvre in their everyday life
· To take a critical stand on the information they get in the advertisements
Instructions for the teacher trainees
As an introduction the following sheet was sent to the teacher trainees by e-mail:
Problem solving in connection with brochures and commercials
Subject: Mobile phones
Aims: As presented above
Description: The pupils in the seventh class are presented with a problem where the necessary data for the solution of the problem are contained in a commercial.
Instructions for the pupils: The pupils receive several commercials and are asked questions about them. They have to make use of mathematics to come up with an answer. Then they are asked to make their own, maybe more descriptive, commercial.
Assignments for the teacher training students:
· How can you organize the lesson for the pupils?
· What questions should be asked?
· What precisely do you want the pupils to do?
· How many commercials would you show the pupils or should they possibly find some themselves?
· Are the pupils better at solving real problems than solely technical ones?
· Which difficulties do you anticipate in connection with the lesson?
· What do you expect the pupils will get from this lesson?
· What sort of performance can be evaluated and how in this lesson?
· Which similar problems can be treated in this way?
· Further: You may bring some mobile phone commercials yourselves.
The course of the lesson with the teacher training students
The number of teacher training students is 25. They study in the third year at Skårup Seminarium to become teachers. One teacher trainee has prepared an introduction to mobile phone prices, on subscriptions, on voice charges and on text messages. This introduction lasts the whole lesson.
Preparing the lesson [This part was video recorded]
The teacher trainees worked in groups to
plan the lesson, which also lasted an hour. Fragments from the presentations of
the teacher trainees’ group work are reported in the following.
![]() Video 1
Video 1
Group1
As a loan or buying. Two different subscriptions. Which one will they choose?
Group2
Different advertisements and three different requirements. Each group is going to have one advertisement and three requirements. The group is to prepare an algorithm for the price and a graph. After this the groups are going to compare the prices. They objectify it to get the text transformed into something useful.
Which one is best for you?
It looks like a storyline.
If we had more time the problem could be more open.
Group3
The pupils are shown a lot of advertisements.
The pupils are going to work with their own requirements, and arguing for their choice of telephone.
The pupils should be placed in groups, where they are going to prepare graphs of their requirements for the different telephone companies. After this they should prepare their own advertisements.
In speaking: the groups of pupils are
going to argue for their choice of telephone in plenum.
![]() Video 2
Video 2

Photo 1. Teacher trainees present their groupwork
Finally the whole team discusses how to make the lesson including the conditions for the lesson with the pupils:
· The teacher training students do not know the pupils.
· There is only one lesson available and no time for reflection.
· The pupils have not learned about the notion of function.
· The teacher training students decide to choose both subscription and need for voice and text because of the limited time together with the pupils. They also select to control the lesson very tightly.
Fragments of the plenary discussion:
![]() Video 3
Video 3
· Everybody wants the pupils to make a graph.
· Because not everyone has a mobile, the pupils should have fictitious requirements.
· Which factors should be kept as variables?
· Is there time for the pupils to be critical?
· Final selection.
· Dialogue about prices in general.
· fictitious requirements and a graph presenting this.
· How are they going to draw the graph?
· How much work are the pupils able to do in the given time?
· Each group gets one advertisement.
The introduction they made is shown underneath (the students’ introduction to the pupils).
Further the pupils must draw a bar chart on a piece of paper by hand to visualize the situation.
Finally the teacher training students need time for discussion.
Five students volunteer for teaching the pupils. One of them wants to make the introduction and there is then a student each for each group of children, as the students’ plan that the pupils should work in five groups of four.
As the teacher training students have relatively limited class time they choose to guide the pupils by having a relatively fixed introduction. The children are still shown the commercials, but do not need to select the information themselves.
The teacher training students’ introduction to the children:
Mobile mathematics in the 7th class
At first, a common introduction in the class.
The class is divided into 5 groups:
· Group 1: Company one
· Group 2: Company two
· Group 3: Company three
· Group 4: Company four
· Group 5: Company five
Each group gets 3 fictive needs and one subscription. From this they should calculate which need best suits their subscription.
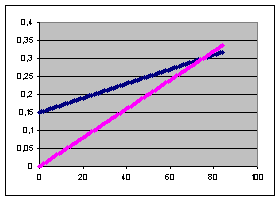
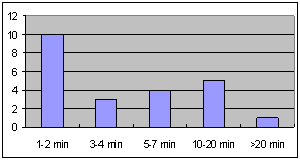
Need 1: 10 minutes voice + 600 text messages (blue in Picture 1).
Need 2: 1 hour voice + 200 text messages (red in Picture 1).
Need 3: 3 hours voice + 60 text messages (green in Picture 1).
Each group produces a bar chart showing 3 different needs according to their subscription.
Finally we will possibly discuss the price differences in the class.
Example of what is expected as the pupils’ outcome of the lesson
To provide understanding the following example showing calculations and column diagram is inserted.
The price at company two is:
· 0,75 DKR/min voice
· 0,20 DKR/text
From these data the pupils should calculate which subscription suits their needs best.
The prices for group two would then be:
Need 1: 10 minutes * 0,75 DKR/minute + 600 texts * 0,20 DKR/text = 127,50 DKR
Need 2: 60 minutes * 0,75 DKR/minute + 200 texts * 0,20 DKR/text = 85,00 DKR
Need 3: 180 minutes * 0,75 DKR/minute + 60 texts * 0,20 DKR/text = 147,00 DKR
The bar chart will look like the one in Picture 1.
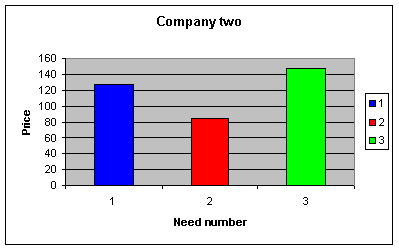
Picture 1. Bar chart showing final costs
There are twenty pupils aged about 14
years. The school is Øster Åby Free School situated a
little north of Svendborg. The math teacher of the class is present but only
observing. Present were six teacher training students, one made the
introduction and one each helped each of the five groups.
![]() Video 4
Video 4
The pupils were concentrated on their work. The corporation between the pupils and the teacher training students was good and the teacher training students did not take over the initiative but let the pupils be active and put helping questions to assist the pupils to come a step forward if they stopped. The pupils calculated how much their assigned subscription would cost with the three given needs. Further the pupils quickly drew the planned diagrams. In this way they got time to look at some of the other subscriptions, which gave them a good basis for the following plenary discussion.
Finally the pupils discussed with the
teacher training students which subscription out of five they would choose and
further which subscription they had actually chosen themselves and the reason
for that.
![]() Video 5
Video 5

Photo 2. Pupils work in the classroom
Feedback to the teacher trainees
At the end of the lesson with the pupils
the trainees were asked what they thought about the lesson and they said it had
been good.
![]() Video 6
Video 6
The mathematics teacher of the class said that the pupils had spoken positively about the lesson.
To have a basis for a dialogue I had handed out an evaluation scheme to the teacher training students. This scheme can be seen here including some of the remarks from the teacher training students.
Evaluation of the lesson about mobile phones
All students were asked to fill in all points for the lessons in which they had participated:
|
Task |
What was good? |
What was bad? |
Remarks |
|
Preparation for the children |
Initial preparation in small groups bringing more input to be presented in the “big” group. Good having somebody to discuss with. Good group work creating many ideas. Fine progress in which everybody brought their ideas. |
Maybe somebody did not express their ideas and just agreed with the others? |
Possibly make an agreement beforehand about how the final selection will take place. Let every “small” group write a page with its proposal |
|
The pupils’ learning |
Good to work in groups, but there is always somebody just “hanging on”. |
We should make a common agreement on what to do when the fast ones are finished.
|
Some finished very fast but others not. Difficult to differentiate and make sure that everybody understood. |
|
What did you learn from the lesson? |
Experience in planning and accomplishment. |
|
|
Table 2. Evaluation scheme for teacher trainees
Further the teacher training students were asked how the evaluation of the pupils could look like. One of the answers looks as follows.
I think that the pupils must only evaluate the elaboration of the instructions and not if they have got a technical result, which I believe should be measured through similar problems.
The evaluation could be:
What is it like to work in groups on mathematics? Why?
How do you prefer to work? – Why?
What is it like having so many teachers around? – Why?
The evaluation discussion takes place in the class 10 – 15 minutes later within the same groups as the children worked in.
Description of another teaching practice situation
At the beginning of the study year 2004 we worked with linear functions at the teacher training institute. As one of the many specific examples we chose to work with payment in connection with mobile phones.
Later one of the teacher training students used this example in her third year of the teaching practice. I visited her in the class when they treated this subject and recorded the lessons on the video. The lessons took place in the sixth class in one of the schools in Svendborg.
All pupils learned something within the two lessons, but the differences were very big. Some pupils could draw the diagrams for two different subscriptions with help; others could not draw a diagram even for the simplest linear function, but were then able to take the first step towards the variable expression. Most of the pupils were in the middle group between these extremities. If the pupils should work with this before treating linear functions the situation must be very simplified:
It should only concern whole numbers and only one variable.
This topic should possibly be treated later but may contribute to a developed education differentiation as it contains a lot of possibilities in what you may include in the calculations.
The teacher training students decided to guide the lesson fairly tightly because of the limited time available.
The pupils were good at carrying out the operations they were asked to and were also able to convert the results to be used in reality.
One of the factors I, as a teacher trainer, want to strengthen is to develop the pupils’ ability to read a text and make a mathematical model out of the text. Unfortunately we did not have time enough to carry out this task. This would be the first step in using mathematics in daily life. A general question in this connection would be if pupils were able to transfer subjects learned in school mathematics to daily life. I often experience that teacher training students separate knowledge learned in one subject or even part subject from what they learn in other places and that the transfer value from one part of their life to another is even very small.
If the pupils often could use mathematics on relevant problems, the engagement and with that the ability to remember and use mathematics would increase. With this also the possibility that the pupils when they have finished school could use mathematics in their daily life would increase.
Even within the school system I have many times experienced that it looks like all knowledge is lost. I have seen that students in upper secondary school seldom were able to use their school mathematics and following I have experienced that our students at the teacher training institute were not able to use mathematics learned during their upper second education. Maybe they would have remembered the mathematics if there had been a higher engagement and less teaching by routine. Routine work is needed, but it should not be the only and dominant way.
Because of the great number of variables it would be more relevant to use spreadsheets.
In Denmark it may be the following variables:
Phone cost – Monthly charge – Minute charge – Call charge – Video charge – Text charge – Included charges
The price is a function of many different variables, which makes it very difficult for most people to determine what will be the best buy for their own needs.
With a spreadsheet you can observe very quickly what happens when we change variables and get a visual picture of what happens by such a change. For the pupils the picture of a change will often drown in time demanding calculations.
Both for me as a teacher at a teacher training college and for the students it has been very fruitful to be so directly involved in planning the lesson in a school class. Normally trainers are rather involved as advisers than participants in the teaching practice of their trainees: the experience for me with this project means that I will try to change this. It has been very relevant to follow the process from the trainees’ first learning through the preparation and to the teaching in the school. The trainees’ engagement and reflection have been very great. More students than normally are active when they can see the direct relevance.
I wish that the whole teacher training is based on regular interaction between theory and practice.
Thanks to Øster Åby Free School, seventh class and their mathematics teacher, Brian M. Østergård.
Also thanks to my mathematics class 22.4 at Skårup Seminarium for their kindness.
by Franco Favilli
University Centre for Educational Research and Training – CAFRE
University of Pisa, Italy
and Carlo Romanelli
Istituto Comprensivo “E. Pea”, Seravezza (LU), Italy
Within the framework of the LOSSTT-IN-MATH project activities, the didactic proposal Cell phones was prepared and presented for discussion to student teachers. The proposal was later piloted by two pairs of trainees in two lower secondary school classrooms.
Among the mathematical notions necessary for the comparison, special attention was paid to proportionality, arithmetical progressions, functions, graphics, approximations and basic elements of statistics. During the classroom activities, pupils also made use of the Excel software.
The Cell phones proposal seems to correspond with a good way of dealing with mathematical notions, introducing them through a nice mixture of theoretical and practical activities. Expanding and deepening could easily lead the discussion well beyond the standard content of a lower secondary school mathematics curriculum. Its piloting requires therefore, first of all, the definition of specific didactic aims and the selection of only a few of the possible mathematical notions for introduction or further use (if they are already available to pupils).
The trainees work in twos or threes. The trainers give each group several tariff plans for mobile telephones calls and ask them to compare different tariffs. Each group is then asked to identify the most convenient tariff plan for the average use of the mobile phone. All the different choices are finally presented and justified in front of the other groups.
The same scheme should be used both by the trainers with the trainees and by the trainees with the pupils at school.
The plan of the piloting was designed and developed in the following scheme:
|
Steps |
|||||||||
|
Trainers (10h)
Preparation of the didactic proposal |
Trainers and trainees (4h)
Introduction Group work Discussion |
Trainees (2h) |
Trainees and pupils (2h)
Introduction Group work Discussion |
Trainees (2h) |
Trainees and trainers (4h)
Reporting Discussion |
Trainees (4h) |
Trainers (5h)
Final report |
||
|
Objectives |
In-context methodology |
|
|||||||
|
Short term
Long term |
Knowledge Competences
Methodology Socialization |
Thinking it over Lesson planning |
Trainees
Knowledge
Methodology |
Pupils
Knowledge Competences
Socialization |
Thinking the lesson over Report |
Trainers
Socialization
Methodology |
Trainees
Methodology |
Thinking it over – Remarks Finalizing the lesson plan Report to trainers |
|
Table 3. Plan of the piloting
Number of trainers: 2 (a university and a lower secondary school teaching staff)
Number of trainees: 42
Number of classes involved in the piloting: 2 (3rd class of lower secondary school)
Number and age of pupils: 40 pupils aged 13
Number of adults in each classroom during the lessons: 2 trainees (present for the first time in those classrooms) and the teacher
The educational aims of the proposal can be roughly divided in general and content aims.
Among the general aims we can consider:
· Making the pupils better aware of the use of mobile phones and the need of critical choices.
· Setting a questionnaire.
· Promoting cooperation in problem-solving activities.
· Increasing the knowledge of terms from economics, finance and commerce.
· Involving the pupils’ families in the educational activity.
Among the mathematical aims we can consider:
· Making the teaching and learning of mathematics more attractive and effective through investigation and evaluation of daily life needs.
· Identifying a problem to be solved by a statistical survey.
· Starting from a real problem, introducing or consolidating basic statistical concepts, such as population, data resources, data collection, statistical units, data organization, representative and non-representative data samples, frequency and percentage, statistical indexes, their representation by and interpretation through graphs.
· Starting from a real problem, introducing or consolidating basic mathematical concepts, such as function, graph of a function, step function, arithmetical progression, direct proportionality, approximations, and equation of a straight line.
· Improving basic technology education of the class, and the disadvantaged pupils in particular.
For the trainees
Planning a unit always requires the teacher to make methodology and didactical choices. As regards the Cell phone proposal, its preparation by the trainers, its piloting with the trainees first and with the pupils after, the discussions during the training sessions, made both trainers and trainees aware of the relevance, for the piloting itself, of the different possible answers to questions and issues such as the following ones:
· What kind of tariff plan have you got for your mobile phone?
· Have you ever considered comparing your plan with others, recently introduced?
· Have you ever tried to evaluate the actual cost of your average call per minute?
· What does average call mean for you? Compare your meaning with other pupils in the group.
· Are you aware of the amount of variables that make such a calculation possible?
· Do you think it is easy to calculate such a cost?
· What kind of knowledge do you need to calculate that cost?
· Make a list of mathematical and statistical notions that, in your opinion, are necessary.
· Which of them could be found in a lower secondary school mathematics programme?
· Try to identify at least two tariff plans that could allow thirteen-years old pupils to calculate the cost of an average call from their mobile phone with such tariff plans.
· Make a comparison of the graphs (x = min, y = €) of two tariff plans.
· Maybe you need to fix some variables…
· Try to prepare a mathematics lesson plan for a lower secondary school class.
· What about submitting a questionnaire to the pupils to introduce them to the topic, thus making them aware of its complexity? You would have a better knowledge of the class context.
· Maybe you could start modifying a tariff plan, thus obtaining something quite simple.
· Are you considering the use of software such as EXCEL to process the different information and use this to draw the graphs?
· What kind of approximations will you make use of?
· What kind of links could you make to other school subjects?
· What kind of application of this problem-solving proposal could be possible in an upper secondary mathematics classroom?
For the pupils
· How much money do you spend on the mobile phone in a month? Make a comparison with your classmates.
· Do you know which tariff plan you have? If not, call your mobile phone operator and ask for the details of your tariff plan!
· Let us compare the information you have obtained about your tariff plan with this one (see Figure 1 below).
· Which of them is more convenient for your average use of the mobile phone?
· How long should an average call last to make your fare plan more convenient?
· Have you ever tried to make any similar comparison?
· Can you imagine that it is possible to make a more accurate comparison of the tariff plans with the help of mathematical notions?
· Will you look for a different fare plan?
· Try to identify a tariff plan that could better fit the needs of your group members.
· Draw a new tariff plan that would be ideal (and realistic!) for the whole group.
· Are you satisfied with the experience? Why?
· Why, in your opinion, did your teacher propose this activity to you?
· Make a report of the activity.
The trainees were grouped in pairs (see Photo 3). The trainers gave them several
different tariff plans (available on the Internet) for the mobile phone calls
for comparison. The trainees were then asked to identify the most convenient
tariff plan for their average use of the mobile phone.
![]() Video 1
Video 1

Photo 3.Trainees working in pairs
At first, the trainees identified different
variables to be considered for the mathematization of the problem and made a
list on the blackboard
![]() Video 2.
The complexity of the problem emerged quite easily.
After an agreement on the variables to be considered, thus making a partial use
of the information available from the tariff plans and partly modifying them,
their comparison was sketched on the blackboard, through Cartesian graphs.
Video 2.
The complexity of the problem emerged quite easily.
After an agreement on the variables to be considered, thus making a partial use
of the information available from the tariff plans and partly modifying them,
their comparison was sketched on the blackboard, through Cartesian graphs.
Taking into account the university careers of the trainees (non-mathematical scientific graduation), the need for better knowledge, especially of certain mathematical and statistical notions was clearly seen. Therefore, the trainers provided them, on the spot, with basic information needed to carry out the task that the trainees were about to do.
The trainees were then asked to think about a possible structure of the lesson plan on this topic in a lower secondary school. After a long and profound debate, first in groups and later in the whole class, two pairs of student teachers agreed to prepare and pilot a lesson plan and to report their experience back to the class.
At the end of the session the trainers gave the trainees further tariff plans and examples of possible mathematical questions arising from their application.
Before piloting the proposal at school, the
two pairs of trainees met, thought over the activities in the training session
and agreed to introduce the problem in a better, motivating way – by setting
the pupils of two classrooms a questionnaire dealing with their use of mobile
phones. Pupils were also asked about their parents’ role in making choices
about mobile phones and their behaviour. The analysis of the answers obtained
in the classrooms proved how poor was the pupils’ awareness of the actual cost
of their calls and of the different variables influencing it. And what is more,
how poor was their interest to look for a tariff plan that would be more
suitable for their needs
![]() Video 3.
The questionnaires analysis was supported by the use
of Excel software.
Video 3.
The questionnaires analysis was supported by the use
of Excel software.
Later on, the pupils were given tariff
plans that the trainees had adapted for the specific educational context so
that they could be more easily interpreted and used for the problem-solving
activity. The pupils worked in pairs.
![]() Video 4
Video 4
Mathematical and statistical notions were used (see Aims) mainly in the construction of the graphs and the analysis of the different needs and habits shown by the pupils in their responses. Different types of graphs were used for the statistical analysis, as shown in the figures below:
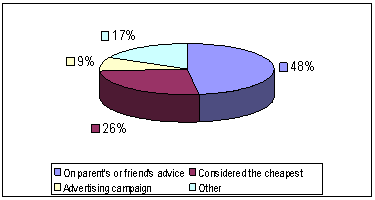
Picture 2. Motivation for the tariff plan choice
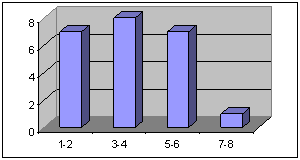
Picture 3. Average calls per day/pupils Picture 4. Average length of the calls/pupils
The role and importance
of numerical approximations and different stages for their introduction when
computing the costs necessary for the tariff plans comparison clearly emerged,
as reported by a student teacher: some pupils have approximated the numbers at the
end, after having made the computations always using non-approximated
values, some others have soon approximated the numbers they had obtained and
have made use of these approximated values for the following computations
(see Photo 4). It was
nice to show, during the debate in the classroom, how such differences could
imply a different evaluation of the most convenient tariff plan.
![]() Video 5a
Video 5a
![]() Video 5b
Video 5b
![]() Video 5c
Video 5c

Photo 4. Approximations at different stages
The piloting also showed that it is possible to introduce the notion of arithmetical progression even in lower secondary schools (see table and graph in Picture 5).
|
Minutes |
Toll at the answer y = 0,15 + 0,002•x |
No toll at the answer y = 0,004•x |
|
|
0 |
0,150 |
0,000 |
|
|
1 |
0,152 |
0,004 |
|
|
2 |
0,154 |
0,008 |
|
|
3 |
0,156 |
0,012 |
|
|
4 |
0,158 |
0,016 |
|
|
5 |
0,160 |
0,020 |
|
|
6 |
0,162 |
0,024 |
|
|
7 |
0,164 |
0,028 |
|
|
8 |
0,166 |
0,032 |
|
|
9 |
0,168 |
0,036 |
|
|
10 |
0,170 |
0,040 |
|
|
11 |
0,172 |
0,044 |
|
|
12 |
0,174 |
0,048 |
|
|
13 |
0,176 |
0,052 |
|
|
14 |
0,178 |
0,056 |
Picture 5. Arithmetical progressions and their graphical representations
The notions of linear function and step
function were illustrated through their graphical representations (see graph in
Picture 6), thus making it possible for each pupil to better evaluate, in relation to the individual average use of the mobile phone, the advantage of choosing a tariff plan based, for example, on the proportionality between cost
and time, instead of a tariff plan based on time units, or vice versa.
![]() Video 6
Video 6
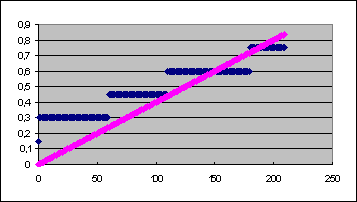
Picture 6. Comparing tariffs (linear function vs. step function)
It is important to mention that, as expected, some pupils found it extremely difficult to use Cartesian coordinates with different measure units for the x, y variables.
After the piloting, the four trainees met again to reflect on the experience and prepare the report for the other trainees. In view of this, they also watched the video recordings made during the classroom activities. To prevent pupils from feeling uncomfortable with another adult in the classroom, the lessons were video recorded by one of the pupils.
It was agreed that, besides the two trainers and all the trainees, two pupils would participate in the feedback session.
The four trainees presented the school
piloting, made comments and remarks, and showed the most important video-clips
taken in the classrooms
![]() Video 7a
Video 7a
![]() Video 7b
Video 7b
![]() Video 7c.
Most of the above described outcomes from the piloting
were introduced for discussion (see Photo 5).
Video 7c.
Most of the above described outcomes from the piloting
were introduced for discussion (see Photo 5).
Photo 5. Tables and graphics from the trainees reporting
Unfortunately, not so surprisingly, while the two pupils were active in the discussion, the non-piloting trainees only occasionally entered the debate.
It is a matter of fact that the two pupils soon seemed to feel comfortable in the new (for them) educational context. Apart for some interesting comments and general appreciation of the proposal they had actively contributed to pilot, the pupils made it explicit that they were all surprised, in the class, by the large amount of mathematics involved in the supposed-to-be easy problem and, as a consequence, by its complexity. As was expected, the trainees acknowledged the possible use of the proposal in an upper secondary school. This would enable the introduction of further mathematical notions and the production of examples of problems in the field, for example, of linear programming and optimization.
After the feedback session, the four trainees met again and, making full use of the piloting activity, further developed the joint report to the training class, structuring it independently and with additional personal comments and remarks, in the form of a Unità di Apprendimento (Learning Unit). This is a teaching methodology recently introduced by the Italian school reform. The Learning Units were used by the four trainees as a part of their work to be evaluated during the exam at the end of the training course.
The class includes 22 pupils, 14 and 15 years old. It is composed of 11 girls, 11 boys. It is the fourth year of secondary school in France.
· To intelligently organize calculations about numerical magnitudes (exact or approximate calculations). To use wisely a calculator, spreadsheet and graphics package.
· To invest knowledge about proportionality using a real-life situation where the proportional model may be questioned.
· To represent numerical data with a bar chart; in a coordinate system: choice of coordinates, of scales, of units, ways of representing the above numerical data.
· To use a specific word list: abscissa, ordinate, proportional ratio, chart …
· To propose a situation both mathematically relevant and familiar to pupils, to motivate the use of language and the use of algebra, particularly linear functions, linear equations and inequalities.
· To introduce pupils to linear functions through the study and the writing of literal formulas: status and roles of the letter, of the equals sign, of a literal expression.
· To work in a group: to listen / exchange / share / produce.
Five telephone FIXED PRICE contracts: 2 hours and sms
Company 1: 36 €, 100 sms given and then 0,07 € per sms
Company 2: 29 €, and then 0,12 € per sms
Company 3: 36,5 €, and then 0,10 € per sms
Company 4: 21,85 €, and then 0,09 € per sms
Company 5: 19,90 €, and then 0,09 € per sms
Three users:
David: 1 hour and 600 sms
Marie: 2 hours and 200 sms
Simon: 1 hour 30 minutes and 60 sms
Five groups:
The class is divided into five groups of four or five pupils, mixed ability, squaring with the five telecommunications companies. Each group has a hardback company file with the following documents:
· A short advertising slogan describing the fixed-price contract proposed by the telecommunications company.
· Examples of charts and graphs.
· Extracts of individual searches made by pupils two weeks ago.
· Graph-paper sheets.
· A transparent graph paper sheet.
The sequence took place on Friday for 2 hours and on Monday for 1 hour:
Five groups are formed by the teacher.
On Friday: The teacher presents the theme and the title of the work “Telephone fixed price contract study”.
Immediately some pupils propose some telecommunications companies and their usual prices.
The teacher gives the instructions orally:
Firstly each group has to compare the telephone bills of the three users referring to the telecommunication company represented by the group. Results will be submitted with a bar chart on the graph paper transparency.
The teacher then writes the instructions on the board.
This first phase lasts for about 35 minutes. The first discussions are about the meaning of the verb «to compare», use of graph paper, choice of magnitudes, of units and graphs. Systematically all the pupils use their calculators. The meaning of operations and results is discussed, particularly the use of approximate calculus, and for some groups proportional processing, or not, to calculate the price of David’s and Simon’s telephone usage.
Secondly two pupils of every group present their prices and their outputs on a graph paper transparency, with an overhead projector. At the end of each report, a discussion begins between the group and the class. This second phase lasts 15 minutes.
Thirdly every group ranks the five telecommunications companies, from the cheapest company to the most expensive one, for each user. The results will be presented in a coordinate system. The X-axis will show the number of sms sent and the Y-axis the amount of the telephone bills in €. Four copies of the coordinate system are given to each group. Only one of these four copies is required at the end of the activity.
Exchanges and work are organized more effectively. Sharing results is necessary within every group to carry out the instructions. This activity lasts 20 minutes.

Photo 6. Pupils are working in groups
On Monday. During forty minutes, within each group, pupils tackle many questions which arouse oppositions or agreement.
· How to distribute calculus better, among them? Is it possible to round up the results? Is it necessary to take into account the telephone usage or only the sms?
· What type of graph to use? In what direction to take the co-ordinate system given by the teacher? Must points placed on the graph sheet be joined or not? What unit on X-axis? On Y-axis?
· How to distinguish, in a same co-ordinate system, telephone companies from users? Whether to use colours, codes, captions, or not?
In each group, mathematical work was organized in two ways: the fifteen calculations and the graphic representations. Distribution of tasks and time management were specific to each group.
At the close of these two sessions, many pupils expressed their satisfaction describing the work as a “new and interesting subject, not only about mathematics, far off square roots”, “more help between them”.
The various graphs and work produced by the five groups showed an important mathematical reflection and good output. However, the mathematical thought processes used by pupils are naturally more numerical than algebraic. So, to become acquainted with linear functions a further sequence is necessary. Then, algebraic language, in particular, will be developed making it necessary and useful to produce and handle literal formulas. So, the next stage of this initiative has to lead pupils to identify the two parts of an algebraic expression – “procedural” and “structural”.
Olivier Arrouch, class teacher.
The subject has been chosen, because it is a major part of pupils’ every day life. The pupils are therefore motivated for ‘problem-solving’ and can be able to transfer mathematical skills more easily than when taught mathematics only through text-books.
The comparison of different tariff plans available for mobile phone calls is a natural matter of discussion even for pupils in lower secondary schools. While comparing, pupils rarely support their opinions by reasoning that could, even unintentionally, be related to the graphic description of the tariff plans they are considering. They hardly understand that for any correct comparison, several mathematical notions are necessary. Whereas some of them are already available, others still need to be introduced.
The general scheme at the two first piloting institutions is seen in the introduction. In Paris the piloting was a part of this, the piloting in the classroom.
The comparison will be with the two first piloting institutions, when only the teacher trainer and the teacher trainees are involved and include Paris, when the pupils are involved.
The common frame for the piloting
· Presentation of the proposal for the teacher trainees
· Teacher trainees get or find themselves several tariff plans
· They are, in groups, asked to make a lesson plan for pupils
· In these groups they discusses the best way to introduce and carry through the lesson for the pupils
· These plans are presented in front of the other groups
· Some trainees are selected to the piloting in the classroom
· Introduction
· Each group is given several tariff plans for mobile telephones calls
· The groups are asked to compare different plans
· In this comparison are asked for calculations and visualisation in form of a bar chart or the graph for a linear function
· Presentation in front of the other groups
· The mathematics notions involved: in Skårup the notion of variable was used in the treatment and the pupils were drawing a bar chart by hand.
· In the two other piloting institutions the subject was an introduction or consolidation of mathematical concepts as function, graph of a function, direct proportionality, equation of a straight line and the use spreadsheet in the treatment.
· The use of spreadsheet is a very good idea you can change the variables and quickly see what happens, which is useful here with the great amount of variables.
· In the second piloting institution the basic statistical concepts were introduced too.
The subject contains a variety of possibilities for using mathematical skills in problem-solving. It is possible to choose how complicated the problem-solving to be, by deciding how many variables to be introduced.
If the competences of problem treating and modelling should be really developed it is important to let the pupils evolve their strategies themselves, without interfering more that absolutely necessary.
© LOSSTT-IN-MATH Project