by Franco Favilli
University Centre for Educational Research and Training – CAFRE, University of Pisa, Italy
and Carlo Romanelli
Istituto Comprensivo “E. Pea”, Seravezza, (LU), Italy
Geometrical discourse requires good knowledge and mastering of the terminology and the notions. On the other hand, the acquisition of geometrical concepts by the learners is facilitated when the communication is supported by the balanced use of graphical language, natural language and geometrical language.
In the proposed activity the learners are asked to work in pairs, one of them providing the other with a sequence of instructions for the drawing of a geometrical figure. Both learners are then asked to describe the figure and to define it.
This geometry teaching activity can represent an interesting opportunity to underline the need to promote the use of different registers of representation and their coordination through specific tasks aimed at converting one into the other.
Through this didactical proposal, the trainees can also directly realize how sophisticated and challenging the transition from the description of a geometrical figure to its definition is for the learners.
This proposal was prepared and piloted at the University of Pisa. It was also piloted, at the same time, at the University of Siena and, later on, at the IUFM of Paris.

The Geometrical puzzles proposal seems to correspond with a good way of dealing with mathematical notions, introducing them through a nice mixture of theoretical and practical activities. Expanding and deepening the idea could easily lead the discussion well beyond the standard content of a lower secondary school mathematics curriculum. Its piloting requires therefore, first of all, the definition of specific didactic aims and the selection of only a few of the possible mathematical notions for introduction, or for further use (if they are already available to pupils).
At the beginning of the lesson, learners receive a sheet of paper (the Learner’s Guide, see Appendix A1) with some explanation about the content and the rules for the didactic activity. The basic rules are:
· Learners work in twos.
· A member of each pair is given a piece of paper with the name of a (plane or solid) geometrical figure that must be kept secret from the partner until the end of the activity.
· The first learner provides the other with a sequence of instructions how to draw the figure.
· Only unitary instructions that correspond with a single graphical activity of the partner are allowed. For example, the instruction “Draw a segment” is allowed, the instruction “Draw the axis of the segment AB” is not allowed, because it requires the determination of the middle point M of the segment AB first, and the perpendicular in M to AB after.
· Each instruction given/received is written on a sheet of paper by both learners.
· If necessary, an instruction can be repeated, but neither modified nor explained.
· For the drawing pupils make use of a sheet of squared paper and a pen (no pencil, ruler, compasses, etc.). No deletions are allowed.
· The in-progress drawing cannot be shown.
· When the sequence of instructions has come to an end, the final drawing is shown and compared with the name of the given geometrical figure.
· Both learners are asked to give the name, the description and finally the definition of the geometrical figure.
· Discussion in the whole class, rooted in the final drawings and the given directions, concludes the activity.
The same scheme should be used both by the trainers with the trainees and by the trainees with the pupils at school.
In Pisa, the plan of the piloting was designed and developed in the following scheme; the hours represent the duration of each step:
|
Steps |
|||||||||
|
Trainers (10h)
Preparation of the didactic proposal |
Trainers and trainees (4h)
Introduction Group work Discussion |
Trainees (2h) |
Trainees and pupils (2h)
Introduction Group work Discussion |
Trainees (2h) |
Trainees and trainers (4h)
Reporting Discussion |
Trainees (4h) |
Trainers (5h)
Final report |
||
|
Objectives |
In-context methodology |
|
|||||||
|
Short term
Long term |
Knowledge Competences
Methodology Socialization |
Thinking it over Lesson planning |
Trainees
Knowledge
Methodology |
Pupils
Knowledge Competences
Socialization |
Thinking the lesson over Report |
Trainers
Socialization
Methodology |
Trainees
Methodology |
Thinking it over – Remarks Finalizing the lesson plan Report to trainers |
|
Table 1. Piloting plan
Number of trainers: 2
Number of trainees: 42
Number of classes involved in the piloting: 2 (2nd and 3rd class of lower secondary school)
Number and age of pupils: 24 pupils aged 12 (2nd class) and 22 pupils aged 13 (3rd class)
Number of adults in each classroom during the lessons: 2 trainees (present for the first time in those classrooms) and the teacher
The educational aims of the proposal can be roughly divided into general and mathematical aims.
Among the general aims we can consider:
· The development of awareness and critical attitudes towards the use of language and its interpretation.
· The awareness of how important it is to use specific and unambiguous language.
· The increase of the learners’ capacity to understand and to elaborate oral instructions.
· The stimulation of “critical” listening to instructions.
· The improvement of the ability of reading, understanding, respecting and applying the rules of the didactical activity.
· The acquisition of the notion of simple instructions.
· The ability to respect the pace of the classmates.
· The capacity to state the reason for the choices made and used during the activity.
Among the mathematical aims we can consider:
· The improved usage of mathematical language.
· The reinforcement of the knowledge of geometrical language.
· The improvement of drawing skills.
· The consolidation of geometrical knowledge.
· The ability to visualize three-dimensional objects from their two-dimensional representations and to represent solid figures on the plane.
· The capacity of describing basic plane and solid geometrical figures by pointing out the properties necessary and sufficient to define them.
· The development of the ability to find a proper balance between the description and the definition of a plane or solid geometrical figure.
· The awareness of the relevance of the definition in geometry.
· The capacity to compare and evaluate different kinds of input from the debate in the context of the correct construction of the concept of geometrical figures.
· Read the Teacher’s guide (see Appendix B) very carefully!
· Make comments and proposals for the modification of the learner’s guide you have received at the beginning of the activity.
· Are the rules stated there clear enough for the pupils?
· When developing the activity in your class, will you use a log-book (i.e. an account of how the lesson developed)?
· How much time should be devoted to the introduction, the development of the activity, and to the final debate?
· Should the didactical activity be presented to the pupils as a role-playing game?
· Considering that the communication, both active and passive, between pupils is quite relevant in this activity, what kind of linguistic register will you use with the pupils?
· Is it important that the pairs of pupils are matched evenly according to their ability?
· As regards the geometrical figure to be drawn, is it better to choose a figure that the pupils already know or a new one?
· What are the advantages and disadvantages of using a known or unknown figure?
· Is it better to use a sheet of squared paper or a blank sheet?
· Only single instructions are allowed. The notion of single or unitary instruction could be quite controversial: make your choice and explain it to the pupils. Why and how?
· What prior knowledge is required for the activity?
· List different possible sequences of instructions for the drawing of the chosen geometrical figure.
· Give examples of possible ambiguous instructions and consequent different drawings and misunderstandings.
· Are you aiming to introduce the definition of the given geometrical figure?
· How could you aid the pupils in the passage from the description of a geometrical figure, through (some of) its properties, to its definition by means of this lesson plan?
· What do you expect from the final debate? What role do you assign to it?
· Will you ask the pupils for a final report of the activity? From individuals or from pairs?
· Make comments and proposals for the modification of the teacher’s guide you have received at the beginning of the activity.
· Did you fulfil the aims you had set for this lesson plan?
· Read the learner’s guide very carefully!
· Be sure to have agreed with your teacher and your friend in the pair about the meaning of a unitary instruction.
· It is not allowed to correct a given instruction or a part of the drawing. Be very careful before speaking or drawing!
· When did you (the person who was receiving the instructions) realize what the geometrical figure was, that had to be drawn? Did it help you? Did you stop executing the actual instructions given by your friend (i.e. you started ignoring them)?
· How much was your prior geometrical knowledge useful?
· How difficult was it to understand the meaning of an instruction? Give at least one example.
· Did you receive any ambiguous instruction? If so, give an example.
· Did you (the person who was giving the instructions) draw the geometrical figure before you started giving the instructions or did you draw it step by step, thus doing what you were asking your friend to do? If it happened, did it help you?
· How difficult was it to find the appropriate words to give an instruction? Give at least one example.
· Are you satisfied with the experience? Why?
· Would you have liked it better to exchange roles with your partner?
· Was it difficult to realize that some properties of the given geometrical figure depend on some other ones? Give an example.
· Why, in your opinion, did your teacher propose this activity?
· Will you make a report of this activity?
· Make comments and proposals for the modification of the learner’s guide you have received at the beginning of the activity.
At the beginning of the session the teacher trainers gave the trainees a blank sheet of paper and the learner’s guide with the explanation of the activity that was about to start. The trainees were grouped in twos and they decided which one had to give the instructions and who had to receive them and make the drawing. The trainees who gave the instructions received a piece of paper with the word rhombus or cube.
As soon as the trainees started the
activity, some of them asked for more explanation about the meaning of the term
unitary instruction
![]() Video 1.
The teacher trainers gave a few more, non
mathematical, examples. Therefore the activity started half an hour after the
beginning of the training session.
Video 1.
The teacher trainers gave a few more, non
mathematical, examples. Therefore the activity started half an hour after the
beginning of the training session.
After another half an hour, when all the
pairs had finished the instructing-drawing-describing-defining activity, the
discussions within the pairs started (see Photo 1).
![]() Video 2
Video 2

Photo 1. Trainees discussing
The following debate in the class was organised in three stages:
· general issues, mainly related to the rules set in the learner’s guide;
· comparison of the outcomes (list of instructions, drawings, descriptions and definitions);
· remarks and comments upon them, as regards the rhombus, first, and the cube, after.
The discussions and the debate lasted three hours, until the end of the training session (see Photo 2).

Photo 2. A trainee reporting for debate
Most of the trainees stated that they had
realized how difficult it was to express in a clear and concise way even easy
mathematical concepts and properties, as an instruction requires, mainly making
only use of natural language and not of mathematical language. The most
difficult task was to find a good balance between the two languages, also
taking into account the restrictions given in the learner’s guide with regard
to the use of mathematical terminology.
![]() Video 3
Video 3
As expected, most of the drawings were
correct
![]() Video 4
Video 4
![]() Video 5,
even if many trainees stated that once they had realized which figure
was to be drawn, they completed the drawing by (almost) ignoring the subsequent
instructions from their partner in the pair
Video 5,
even if many trainees stated that once they had realized which figure
was to be drawn, they completed the drawing by (almost) ignoring the subsequent
instructions from their partner in the pair
![]() Video 6
Video 6
![]() Video 7.
This could be considered a weak
point in this part of the piloting of the proposal, because in such cases it
was impossible to compare the specific instruction with the related drawing. It
would therefore be important to emphasize more and focus the attention of the
learners on the fact that any drawing has to correspond exactly to the given
instructions, no matter if it is right or wrong.
Video 7.
This could be considered a weak
point in this part of the piloting of the proposal, because in such cases it
was impossible to compare the specific instruction with the related drawing. It
would therefore be important to emphasize more and focus the attention of the
learners on the fact that any drawing has to correspond exactly to the given
instructions, no matter if it is right or wrong.
Several ambiguous instructions were
presented during the discussion
![]() Video 8
Video 8
![]() Video 9,
thus allowing the teacher trainers to recall
to trainees’ memory some mathematical concepts and/or to make a few of them
better understood
Video 9,
thus allowing the teacher trainers to recall
to trainees’ memory some mathematical concepts and/or to make a few of them
better understood
![]() Video 10.
It is important to outline here that the university career
of all the trainees in the class was mostly in scientific subjects, but not in
mathematics. They had studied only one or two courses of mathematics in their
undergraduate studies.
Video 10.
It is important to outline here that the university career
of all the trainees in the class was mostly in scientific subjects, but not in
mathematics. They had studied only one or two courses of mathematics in their
undergraduate studies.
The need for a better acquisition of some
basic mathematical notions became evident, as expected, when the discussion
started about the definitions of rhombus and cube. Quite often the relation between the description of the
properties and the definition of a geometric figure was not clear at all
![]() Video 11
Video 11
![]() Video 12
Video 12
![]() Video 13.
It was therefore necessary to spend much time on that and on the difference
between the image/drawing of a geometrical figure and the geometrical figure
itself.
Video 13.
It was therefore necessary to spend much time on that and on the difference
between the image/drawing of a geometrical figure and the geometrical figure
itself.
Two trainees offered to pilot the lesson plan in a second class of a middle school, using the rhombus, and two others offered to pilot it in a third class, using the cube. Before the piloting trainees were asked again by the trainers to make their comments and remarks on the activity and the rules to give to the pupils (12–13 years old) for an effective and useful impact of the piloting, according to the aims originally given by the trainers and the possible modifications just agreed among the trainees. The learner’s guide was slightly modified before entering the classroom.
The trainees decided to work with squared
paper and no geometric tools, such as the ruler and set square (see Photo 3)
![]() Video 14
Video 14
![]() Video 15.
Video 15.

Photo 3. A pair at work respecting the given rules
The most relevant outcomes, similar to the ones with the trainees:
· It was necessary to explain better the meaning of unitary instruction.
· Some instructors said it was difficult to find the right words to structure some instructions (Photo 4), even if they had a clear idea of what they wanted their schoolmates to draw.

Photo 4. A list of instructions
· After a few instructions, most pupils successfully completed the
drawing (almost) ignoring the remaining instructions: some drawings were
correct even if the instructions were wrong (the important thing was to
succeed, to win the game!).
![]() Video 16
Video 16
· The use of the squared paper made the drawing activities easier.
![]() Video 17
Video 17
· Several instructions were ambiguous and, therefore, misleading (see Photo 5).
![]() Video 18
Video 18

Photo 5. Consequences of ambiguous instructions…
The most relevant outcomes, different from the ones with the trainees:
· From the beginning of the session pupils complained about the difficulty of the linguistic register used by the trainees both in the guide and the oral communication.
· Most pupils made good use of letters to identify the ends of the line segments.
· For most pupils to describe or to define a geometrical figure were
equivalent notions.
![]() Video 19
Video 19
· Low achievers greatly benefited from this kind of activity.
· The final debate in the classroom started with each pair presenting their activities to the whole class for the discussion.
· The change of roles within the pairs was an additional activity that pupils wanted to experience with different figures.
Two pupils participated in the feedback session as well as the two trainers and all the trainees.
The four trainees presented the piloting (see Photo 6) with the pupils to their colleagues, making comments and remarks, and showing video-clips from the class.


Photo 6. Trainees presenting the piloting to the colleagues
Most of the above outcomes from the
piloting were introduced for specific discussion
![]() Video 20.
However, it must be said
that, while the pupils were active (see Photo 7) in the discussion
Video 20.
However, it must be said
that, while the pupils were active (see Photo 7) in the discussion
![]() Video 21,
the non-piloting trainees just occasionally entered the debate.
Video 21,
the non-piloting trainees just occasionally entered the debate.

Photo 7. Pupils actively debating with the trainees
Additional issues from the discussion:
· To find the appropriate way to introduce and motivate the aims of the activity.
· To identify the appropriate didactic contract between teachers and pupils for the implementation of the activity.
· To manage the time in the class (the piloting required more time than originally planned).
· To consider the prior knowledge of geometric software as a possible source of help, especially for the pupils who are asked to give the instructions.
· To mark the difference between the rigour of mathematical language and the “flexibility” of natural language.
· To decide how the transition from the description of a geometric figure to its definition can be demonstrated in a lower secondary school.
The activity aimed at making trainee teachers reflect on the different languages, graphical and verbal, that intervene in geometrical discourse and determine its development through their coordinated interaction. It turned out to be an interesting opportunity to underline the need to promote teaching the use of different registers of representation and their coordination in geometry through specific activities for converting one into the other.
Activity developed in the training session
Number of trainees: 18
Total duration: four hours (one hour for work in pairs – three hours for discussion)
The activity was set up following the directions provided by the piloting group in Pisa.
Trainees were grouped in pairs and within each pair the roles of receiver and provider of instructions were assigned. Each trainee was then given guidelines with instructions to follow together with the rest of the material. Before starting the activity it was necessary to clarify the meaning of the expression unitary (simple) instruction included in the sheet through examples to enable participants to draw the figure in successive steps. On the sheets given to those who provided instructions there was the words rhombus, isosceles trapezium or cube. At the end of the first phase, after one and a half hours since the working session began:
· each member of the pair had filled in their worksheet with either
given or received instructions, indicated in writing possible comments and
given a definition of the figure
![]() Video 1
Video 1
· the sheet with both the name of the figure and the drawing made were shown.
The subsequent phase consisted of a collective discussion of the each pairs’ work. The first comments by trainees were about the unexpected difficulties they met in this work, despite their familiarity with the geometrical figures considered. Everybody agreed that the role of instructions provider was more difficult than the role of receiver and executor of instructions: those who gave instructions had to refer to an image and name of the figure they could recall to their minds, to interpret that image both perceptively and cognitively, and formulate appropriate messages for its reproduction. Some declared they did not manage to complete the list of instructions (even after many attempts), others confessed they had difficulties about the way they had formulated them and were not sure they could be understood by their colleague. Then some lists of instructions provided by trainees (and reported on a transparency) were examined and commented upon together with the way these instructions were interpreted and graphically translated by the ones who received them.
In Appendix C, we report some of the worksheets commented in the session with trainees.
This was a chance to reflect with trainees on the two following aspects:
· mathematical language and its role in the process of knowledge construction;
· the role of definitions in geometry.
A. Mathematical language and its role in the process of knowledge construction
An appropriate use of language presupposes
full awareness of the mathematical terms introduced and the indication of non
ambiguous instructions that can be interpreted in the same way by anyone. In
different cases instructions were given that permitted the drawing of figures
with geometrical characteristics different from those we wanted to obtain (for
instance the following instructions: 1. draw a segment; 2. draw another
segment, perpendicular to it in its midpoint, do not lead to a univocal
identification of a rhombus, as they were meant to).
![]() Video 2
Video 2
We had the feeling that the theme of the use of language could offer material for study, although not all trainees fully acknowledged the problem.
Somebody was puzzled by the critical analysis carried out on the given instructions, since they believed that “although instructions are not very precise, the receiver is led to interpret them and complete them correctly”. In certain drawings we noticed that the figures were the intended ones, but it was not possible to deduce them from the instructions given.
The tendency in the presence of wrong or defective messages was to fill the information gaps on the basis of the global message, using perception and regularisation phenomena; in other cases, the initial visualisation of the figure, generated by the initially received information led the receiver to carry on with a correct drawing although instructions were not appropriate[1].
Discussion also led us to reflect on the difference between natural language, characterised by richness and variety of expressions, and mathematical language, in which each term has a specific meaning and this determines its use.
Finally it was remarked that in many cases, a ‘stranger’ element to the figure was introduced in giving instructions: we mean that we used information describing the figure as located in a standard way in the natural reference frame constituted by the borders of the page. This highlighted the existence of stereotypes in the mental representations of concepts and geometrical relationships (in fact, often instructions contain terms like “horizontal” and “vertical”: “draw a horizontal segment”, “draw a vertical segment going through the midpoint”).
The experience made trainees reflect on the need to develop specific activities related to the learning and use of mathematical language in teaching. Although the correct use of language requires a considerable time to mature, it is nevertheless a fundamental instrument for knowledge construction.
B. The role of definitions
Another point for reflection was suggested by the request on the worksheet of giving a definition of the drawn or described figure. This request was interpreted in different ways by trainees: some only indicated the name of the figure and others listed many properties, often more than those needed to characterise it.
As an example, here are some definitions of rhombus given by trainees showing this aspect and which were analysed in the working session:
· Rhombus: “Plane geometrical figure, particular case of a parallelogram with opposite sides pairwise parallel and interior angles pairwise equal, and perpendicular diagonals with different lengths”.
· Rhombus: “Quadrilateral having all equal sides and equal opposite angles”.
· Rhombus: “Parallelogram with perpendicular and not equal diagonals”.
· Rhombus: “Quadrilateral with four equal sides, pairwise parallel”.
We reflected upon the meaning of definition in mathematics and on the difference between properties that describe a figure and properties that define it. In particular, we discussed about how to “minimise” the stated properties in the case of the rhombus, so as to identify those necessary and sufficient to characterise it each time. We noticed that identifying necessary and sufficient properties is a fundamental moment in the construction of definitions, but it certainly marks a delicate and difficult transition moment for pupils. Hence we need to tackle the learning of properties with pupils to construct definitions that make use of specially designed materials[2] and/or of the Cabri software (the construction mode of Cabri highlights which necessary and sufficient properties were considered and therefore which definition is underlying).
We pointed out how the issue of definition is strictly intertwined with that of classification: i.e. properties expressed by the definition must allow one to include in a certain class only the objects that have those properties. We also noticed how definitions given by trainees often led to “classify by partition” (requiring that a rhombus be a parallelogram with perpendicular and not equal diagonals implies removing squares from the set of rhombuses). This was the chance to highlight the fact that Euclid in his “Elements” defines by partition: for example, the definitions of quadrilaterals he gives aim to determine a partition in the set of these figures. The choice we make nowadays privileges definitions that give rise to inclusive relationships, enabling a comparison between geometrical figures that highlights their analogies and differences. When it is necessary to distinguish among concepts (e.g., concave or convex quadrilaterals), one needs to draw on definitions by partition. We discussed the fact that classification by inclusion, although more complex, facilitates a deductive systematisation of notions (particular concepts are a subset of more general ones), is more economic than a classification by partition and makes it possible to give each geometrical object more alternative definitions (a square is a rhombus with equal diagonals or a rectangle with all equal sides).
In teaching, it is fundamental not to anticipate definitions before the construction of the environment in which they get a meaning.
Activity implemented in the classes
Number of trainees: 2
Overall duration of the activity in each class: two hours (one hour for presentation and implementation of the activity– one hour for discussion)
Activities were proposed by two trainees in their classes, respectively a grade 6 class (18 pupils aged 11-12) and a grade 8 class (18 pupils aged 13-14), and in two grade 7 classes (20 pupils and 17 pupils aged 12-13). Each time the class teacher was present.
The two trainees presented the activity to pupils as a game for pairs, named “Discovering geometrical figures”, in which one of the two components gave a list of “clues” which had to lead the other one to “identify” the figure. The pupils’ work was structured as in the training course session. We needed to spend more time than we expected to explain how instructions had to be given (nevertheless we found non appropriate formulations in the written productions). The chosen figures were rhombus, trapezium, isosceles triangle and cube.
In more than one class, pupils wanted to experiment and try both roles within the pair. In one of the classes, the experimenter proposed a modification of the activity to avoid pupils helping each other within the pairs, through an exchange of forbidden information. The following modalities of work were followed: both pupils of each pair were given a sheet with the name of a figure to be secreted (the names of figures in the two sheets were different); each pupil had to write down a list of instructions so that their partner could draw a figure; successively the instruction sheets were exchanged and each pupil could read, comment in writing on the received instructions if they were not clear enough, and draw the figure. At the end they had to give back the sheet with instructions, comments and drawn figure to their partners.
At the end of the activity each pair commented on their work with their classmates and the teacher experimenter.
Collective discussion of feedback
Number of trainees: 18
Overall duration: two hours
Those who worked in the classrooms described their experience.
One point made was about the amazement pupils experienced when facing the proposed activity: it was unusual and they felt unprepared and feared they would be assessed negatively by the teacher. Only after being reassured that it was a game intended to help them study geometry could they feel more relaxed and free to express themselves.
Several pairs, especially in a grade 7
class, were influenced by the fact they “had to” provide a correct drawing of
the figure, and they made it “appear” anyway, although it was incompatible with
the instructions written on the sheet (a clear sign of illegal exchange of
information). Due to this, the teacher-experimenter introduced a modification when
he proposed the activity in the other grade 7 class, asking pupils to play the
same role simultaneously, but on two different figures. Results were, as
expected, more meaningful, and showed a generally good correspondence between
the set of instructions and the drawn figure.
![]() Video 3
Video 3
We also observed that pupils, (as did the trainees in the training session), evaluated the task of giving instructions as the most difficult one and admitted they had doubts about the way they expressed themselves. Those who received instructions admitted they were often in trouble and sometimes they made the drawing after interpreting instructions personally (“If I had not understood what it was I would never get to draw the figure: some data were a bit crazy”).
Some works produced by pupils were examined: they showed different levels of appropriation of the use of geometrical language and in some cases a strong contrast between what they wanted to describe and the way of doing it. Another aspect we pinpointed was the difficulty of giving a meaning to the expression “give a definition of the drawn figure” which for many pupils meant recognising it and writing down its name, and for others, listing some of its properties.
The proposed activity led trainees to reflect upon a number of aspects.
· Difficulty in using mathematical language correctly: uncertainties, doubts and mistakes shown in providing instructions express the need to favour, in teaching, the verbalisation process, which induces students not only to make their ideas explicit but also to try and make it in a clear and correct way to make them understood.
· The need to use the linguistic instrument appropriately, its use is a fundamental step towards the construction of knowledge, although it requires a considerable time for maturation.
· The need to develop activities like this one, because they offer information about pupils’ knowledge, the conceptualisation level they have reached, possible gaps, and misconceptions. This information is fundamental to be able to intervene in the classroom with appropriate and well planned teaching actions.
· The more general need to develop geometrical discourse through a coordinated interaction of different registers (verbal, graphical and symbolic) and the acknowledgement of the important role played by perception and visualisation.
One trainee teacher wrote this comment:
Personally I believe that the activity we carried out was very interesting. Because it is not easy even for those who have a rather deep knowledge of the subject to convert spoken language into graphical language and vice versa. Given that, I think the same activity carried out in a lower secondary school class can raise interest and curiosity in both the teacher and his pupils.
The proposal was also piloted, in a slightly different way, at the I.U.F.M. of PARIS by Catherine Taveau (class teacher: Cynthia Dobin). The class included 28 pupils, 11 to 12 years old, in their first year of secondary school.
The two principal aims of the teacher being the same as in the two previous piloting – to reinforce the pupils’ knowledge of geometry language and to facilitate the transition from the appearance of a figure to its properties (i. e. from what can be seen to what can be known) – the proposal was implemented in two sessions.
First session
The receivers had only to draw the figure by hand, without geometric instruments.
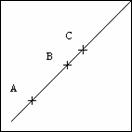
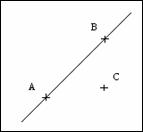
Picture 1. Drawing of lines
Comments – Many pupils tried to write instructions for drawing exactly the same figure (including for example measurements), and in several cases, the instructions were not precise enough, but this didn’t prevent the receivers from drawing the figure correctly.
Second session
This session took place one month later. The teacher gave a geometrical mini-glossary to the pupils and asked the receivers to draw the figures precisely (with instruments).
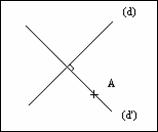
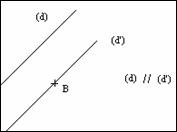
Picture 2. Drawing of “circles”
Comments – The instructions for the first three figures were mostly correct, except for the last one. The teacher decided to extend the sessions with a computer activity, using Cabri Géomètre.
The teacher was very interested in this work, and became convinced of the difficulties for pupils of this age to use precise geometrical language. But it became obvious to her that such tasks (including those with Cabri) are good ways for pupils to understand the difference between describing and defining a figure.
To make pupils better aware about the difference between describing and defining a figure and to lead them towards the concept of definition of a figure, in the first piloting at the University of Pisa, it was decided by the trainees that went to the school:
· at first, to ask pupils to make a list of all the properties they could ‘see’ in the given figure;
· then, to consider each of these properties and to compare it with the other ones;
· finally, to delete the property from the list if they thought it was a consequence of one of the others.
In this way pupils were convinced that the “surviving” properties represented a better, more refined and shorter description of the figure: something equivalent or very close to what their teacher called its “definition”. The discussion in the whole class of the lists produced by the different groups of pupils, in particular the explanations provided to motivate the deletions, greatly contributed to make the introduction of one of the most complex and sophisticated mathematical topics, the concept of definition, both attractive and effective.
It is important to say that the three piloting proved how relevant for the learners (trainees and pupils) it is not only to master the geometric language but also to be able to organise and express an algorithmic process (the set of instructions)[3] to obtain the intended product (the drawing) from another learner who is just expected to execute the instructions. However, the difficulty (or impossibility) already mentioned for learners merely to carry out the instructions given, and the fact that their previous knowledge of the figure often pushed them to make the correct drawing, no matter what instructions were received, show how important it is to introduce the activity pointing out the importance of fully respecting the instructions received, in the way they are given and interpreted. For learners, especially for pupils, the wish to be right or, even, “to win” is too strong to resist any rule!
As regards the unbalance that could be seen in the tasks given to the pair (the instruction provider and the executor) strongly suggests to re-play the activity using a different figure and exchanging the roles in the pair, as it happened in the first two piloting.
SUGGESTED READING
Ellerton, N.F. and Clarkson, P.C. (1996). Language Factors in Mathematics Teaching and Learning, in Bishop A.J. et al. (eds.), International Handbook of Mathematics Education (pp. 987-1033). Kluwer Academic Publishers, Dordrecht.
Favilli, F., Japelt, A. and Novotná, J. (2005). Developing good practices for teacher training focused on understanding classroom environment, in Novotná J. (ed.), Proceedings of SEMT '05 – International Symposium Elementary Maths Teaching (pp. 335-336). Charles University, Prague.
Favilli, F. and Villani, V. (1993). Disegno e definizione del cubo: un’esperienza didattica in Somalia. L’insegnamento della matematica e delle scienze integrate, 16, n.10, 907-925.
Maier, H. (1995). Il conflitto tra lingua matematica e lingua quotidiana per gli allievi. La matematica e la sua didattica, 3, 298-235.
UMI-CIIM (2001). Matematica 2001, Materiali per il XXVII Convegno Nazionale sull’Insegnamento della matematica. Lucca: Liceo Scientifico “A. Vallisneri”.
Materials for
the activity:
it is possible to use
only a sheet of paper, a pen and the form to be completed.
ü Pupils work in pairs. Each pupil in a pair plays a specific role: one pupil (the instructor) gives instructions and the other one (the drawing maker) sketches a drawing, following the instructions received.
|
THE INSTRUCTOR You are going to receive a piece of paper with the name of a geometrical, plane or solid figure, which cannot be shown or told to anybody.
Your goal is to allow your classmate to draw the given figure, step by step through a series of instructions. 1. If you like, you can draw the figure either before or during the game; 2. You can only give unitary instructions, i.e., each instruction should enable your classmate to draw just one single part of the geometrical figure. Let us explain it with a non-mathematical example: should in the sheet of paper be written laid table, the first related unitary (and therefore allowed) instructions could be: Lay down the table cloth – lay down a knife – lay down a fork – … while neither of the following instructions could be allowed: lay the table for lunch – we use it everyday for our meals. 3. Giving the instructions you can use some mathematical words such as segment, axis, angle, etc. but you can not use names of polygons (triangle, square, etc.), geometrical formulas and names of objects that recall the geometrical figure to be drawn (for example, if the figure is a circle, you can not say “Draw a wheel”). 4. Write every instruction on the special form you have received, with your comments, if any. 5. If the drawing maker asks you to repeat the instruction, you can do that only using the same words. 6. You can give the next instruction only when the drawing maker has executed the previous one. 7. When the last instruction has been given and executed, you should write down a description and a definition of the given figure.
|
THE DRAWING MAKER Your classmate is going to receive a piece of paper with the name of a geometrical, plane or solid, figure. He/She will ask you to draw this figure through a series of instructions.
Your goal is to draw the given figure step by step. 1. Write down every instruction you are given by the instructor on the special form you have received, with your comments, if you have any. 2. Should an instruction be not clear, you can ask the instructor to say it again but not to explain it. 3. Should the instruction still be not clear, you can write it down and make your comments on the special form. 4. Execute the instruction and tell the instructor when you are ready. 5. You should not make corrections to the drawing. If you realize that you were wrong, write it on the special form. 6. When the last instruction has been executed, you should write the name, a description and the definition of the given figure.
|
The final drawing can be shown to the instructor and to the whole class only when all the pairs have finished.
Appendix A2: Geometrical puzzles – Instruction Sheet
Pair: __________________________________________________________________
|
Instructions |
Comments |
|
1)
|
|
|
2)
|
|
|
...
|
|
Name of the figure: _______________________________________________________
Description of the figure: ___________________________________________________
Definition of the figure: _____________________________________________________
Appendix B: Geometrical puzzles – Teacher’s Guide
The aim of this guide is to help teachers adapt the teaching activity to the competences of the class where it will be carried out. Since the activity is addressed to lower secondary school pupils, we have to consider that at this age (11 – 14 years) pupils’ mind is just opening on to abstraction. Moving from the concrete to the abstract form is peculiar to this age.
Aims
The activity aims on one hand at strengthening pupil’s ability to use the language of geometry and on the other hand, at developing, the teacher’s ability to construct geometrical concepts in pupil’s mind, without being too much constrained by definitions.
Requested background knowledge
The activity requires that pupils know a few basic geometrical concepts, such as segment, angle, perpendicular and parallel segments.
Complementary teaching materials
The geo-plane is a useful tool for the activity because it can represent a real image of a spatial context. Furthermore, it does not hinder pupil’s free thinking.
Description and remarks
1. The teaching activity is presented to pupils as a game, thus decreasing their anxiety related to a possible assessment and allowing them to live the educational experience without any stress and actively. The activity should be introduced as a role game. There are two, quite different roles:
· the pupil who gives instructions (the instructor);
· the pupil who receives instructions (the drawing maker).
The instructor is given a piece of paper with the name of a geometrical figure and he is supposed to lead the drawing maker to draw it.
2. The speech should fit pupils’ age. Therefore, the teacher should not use the imperative form, that is authoritarian and recalls the language frequently used in the maths textbooks (e.g. calculate the following expression, solve the following problem), but should rather use the first plural person. However, if necessary, the imperative could be smoothened by the use of the interrogative form accompanied by the verb can.
3. For this type of activity pairs should not necessarily be homogeneous, because the objective is communication, both active and passive, between pupils. However, the teacher could form a homogeneous pair at least. In the first phase of the activity work in pairs is important to ease socialization.
4. As regards the geometrical figure to be drawn, the choice might be between a figure that pupils have already studied and a new one. On one hand, the background knowledge of the geometrical figure could reinforce pupil’s knowledge of its properties and ease communication in the pair; on the other hand, it could activate in pupils pre-organized mental schemes. For example, the pupil in the pair who receives the instruction could, at a certain point, carry on with the drawing just because he/she understands which figure is to be drawn and not because of the instructions he/she is getting from his/her peer. Something similar could happen to the pupil who gives instructions, because he/she may hardly understand the different interpretations of his/her own instructions; for example, the instruction draw two parallel sides does not make it clear:
a) whether the sides are congruent or not;
b) which is the distance between the sides;
c) whether the sides have an endpoint on a common perpendicular line or not.
Very likely, the pupil who receives this instruction will draw two parallel sides of a square.
If we use a figure unknown to pupils, instead, they will be more careful in the way they give instructions, as well as in the way they execute them, because they do not have any related mental scheme yet. However, in this case, the activity might possibly be more difficult to pupils.
5. The use of squared sheets of paper can ease the task of both pupils in the pair (the one who gives and the one who receives instructions). However, this could represent a limit because it could suggest pupils’ preferential routes (e.g. the instruction Draw an oblique segment could be followed by the drawing of a segment with 45° inclination, because of the squares in the sheet).
In the case the teacher decides to use a blank sheet of paper, it would be useful to allow pupils to use both the ruler and the square.
Also the pupil who gives instructions should be given a sheet of paper where he/she could draw the figure as well, for a visual support. In fact, at this age (11 to 14 years), pupils have poor abstraction ability and the drawing of the figure according to their own instructions could ease their own monitoring of the procedure.
6. As the activity is based on communication between pupils in each pair, the teacher should focus pupils’ attention onto the fact that only single instructions are allowed. The notion of single or unitary instruction could be quite controversial: it is up to the teacher to make a choice and explain it to pupils. For example, in order to have the diagonals of a rhombus drawn, two different sets of instructions might be given:
a) draw a segment AB – call M its middle point – draw a segment MC perpendicular to AB – draw the segment MD congruent and adjacent to MC (a sequence of four unitary instructions).
b) draw two perpendicular segments intersecting in their middle points (just one non-unitary instruction).
In the activity form given to pupils, it could be useful to provide an example of unitary instruction not from a mathematical context but from daily life, with the aim of making them feel free in developing the activity.
7. At the end of the activity pupils are asked:
a) to write the name of the figure they have drawn;
b) to describe it;
c) to define it.
This last phase of the activity is useful for pupils’ construction of the concept of the given geometrical figure, through preliminary steps towards its definition. Furthermore, depending on the class context, the teacher should choose whether to ask for the definition of the geometrical figure or not.
8. The final debate in the class is an important phase of the activity because it allows the teacher and the whole class to observe the final drawings, to compare the set of instructions and the drawing sketched by each pair, to hear and discuss different ideas about the given figure. In view of that, the following strategies could be adopted:
· at first, a pair should present and describe their activity to the classmates, that are invited to ask questions and make comments, thus creating the conditions for a real discussion among peers;
· after that, a change in the pairs’ composition could be suggested, thus having, for example, the instructor of a pair working with the drawing maker of a different one. This strategy should make pupils understand the importance of using a univocal mathematical language and terminology.
9. Changes to the activity
· To provide all pupils in a class with the same set of instructions for the drawing of a given geometrical figure. Some of these instructions could be given in an ambiguous way, thus allowing for an investigation on pupils’ reaction to different interpretations.
· To ask pupils to work on the drawing of a non-standard geometrical figure.
· To make different groups in the class. Each group choose a geometrical figure and set a sequence of unitary instructions to draw it. The teacher is asked by each group to be its drawing maker and draw the chosen figure.
· To make different groups in the class. Each group gives a set of unitary instructions for the drawing of a geometrical figure to another group and vice versa, as in a contest.
Appendix C: Geometrical puzzles – Two trainees worksheets
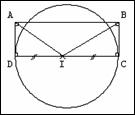
Example 1: Construction of a rhombus
|
List of instructions |
Comments by the receiver |
|
1. Draw a horizontal segment |
|
|
2. Take the midpoint of that segment |
|
|
3. Draw a vertical segment going through that midpoint |
|
|
4. Points of the segment must be equally distant from the segment’s endpoints. |
“You can not understand which segments it refers to” |
|
5. The two segments must not have the same length |
|
|
6. Join the two segments’ endpoints. |
|
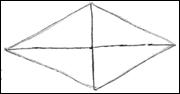
Actual drawing of the rhombus, as obtained from the above instructions.
Definition of the figure (from the instructions receiver) – “Rhombus: parallelogram with perpendicular and not equal diagonals.”
Definition of the figure (from the instructions provider) – “Rhombus: plane geometrical figure which can be viewed as a particular case of a parallelogram with the opposite sides pair-wise parallel, the interior angles pair-wise equal and the perpendicular diagonals not having the same length.”
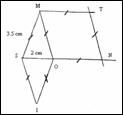
Example 2: Construction of an isosceles trapezium
|
List of instructions |
Comments of those who give instructions |
Comments of those who receive instructions |
|
1. Draw a horizontal segment |
|
|
|
2. Divide the horizontal segment into three equal parts |
|
|
|
3. Label the four points you got on the segment orderly A, B, C, D |
|
“We were not told starting from the left” |
|
4. Trace a segment parallel to BC |
“Wasn’t I clear? I skipped a passage: trace the perpendicular to AB by point B and the perpendicular to CD by point C” |
“I can draw anywhere but I choose to draw it over BC and with equal length” |
|
5. Label the segment EF |
|
|
|
6. Join A and E |
|
|
|
7. Join D and F |
|
|
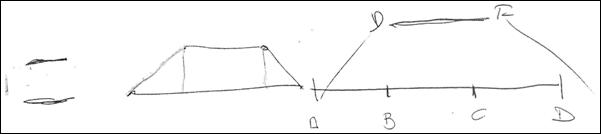
Actual drawing of the trapezium, as obtained from the above instructions.
Definition of the figure: The figure is an isosceles trapezium i.e. a quadrilateral with two differently sized parallel sides and two equal sides. Interior opposite angles are supplementary.
© LOSSTT-IN-MATH Project