by Marie Hofmannová and Jarmila Novotná
Faculty of Education, Charles University in Prague, Czech Republic
The following unit is a part of LOSSTT-IN-MATH project piloted in the CLIL course (Content and Language Integrated Learning, i.e. teaching a non-language subject through the medium of foreign language) at the Faculty of Education of Charles University in Prague (Novotná, Hofmannová, 2000). This two-semester pre-service teacher training course is aimed at students as of the third year of their studies. It is a seminar – 90 minutes per week – with many activities run in the form of workshop.
The course is led by two trainers, one specialised in mathematics education, the other in methodology of teaching English. During the LOSSTT-IN-MATH piloting experiments, the CLIL course was attended by fifteen trainees.
The course was originally designed for teacher training of prospective teachers of mathematics and English language. It is conducted in English. Regardless of this fact, also students – prospective teachers of other non-language subjects and foreign languages participate. This feature enriches the course in the multilingual perspective. The course combines educational theory and teaching practice, bringing students gradually from lesson observation, mastering subject specific vocabulary and CLIL specific knowledge and skills. This is followed by microteaching of peers based on a variety of materials (e.g. textbooks, student-made worksheets) and concluded by a teaching module in real school conditions.
Mathematical content covers mathematics for lower and upper secondary levels and reflects both mathematics taught in public system of education in the Czech Republic as well as some aspects of the bilingual experiment carried out in selected upper secondary schools. From the language perspective, the aim of implementing CLIL is to provide pupils with more exposure. What CLIL offers to learners of any age is a natural situation for language development which builds on other forms of learning.
For the purposes of piloting LOSSTT-IN-MATH proposals, we selected such units that seemed to be compatible with our course content. The activity Lucky Numbers was included in the set of investigative activities proposed by Western Australian Mathematical Association and later modified to combine mathematics and foreign language teaching.
by Marie Hofmannová and Jarmila Novotná
“Choose a number. Square each of its digits and add the squares to get a second number. Square the digits of the second number and add the squares to get the third number. Continue this way to get a sequence. If the sequence reaches 1, the original number is called lucky. If not, it is called unlucky.”
Mathematical topics for development
Arithmetic and application of algorithms
Aims
For trainers:
· Guiding the trainees from theory to practice
· Making the trainees develop a lesson based on a problem taken from a mathematics textbook
· Providing instructions and feedback
For trainees:
· Investigating solving/learning strategies
· Developing a lesson plan
· Preparing own teaching material
· Peer teaching
· Classroom teaching
For secondary school pupils:
· Experiencing the teaching of mathematical content through the medium of English language
· Making problem solving more effective by discovering regularities
· Practising skills of addition and multiplication of natural numbers
Description of the activity
The training activities were planned in five stages, i.e. five weeks. Stages 1, 2, 3 and 5 were carried out during the CLIL course (45-minute sessions), stage 4 in the secondary school (a 45-minute lesson).
Stage 1 The trainees
· solve the problem and compare different solving procedures,
· discuss the necessary knowledge and skills for each solution (from the learners’ perspective in both mathematics and English as a foreign language).
· Homework for stage 2: the trainees prepare the first draft of a lesson plan (for team/peer teaching).
Stage 2 The trainees
· teach one phase of their lesson plan (team/peer teaching),
· analyse the teaching attempts,
· suggest changes and select the best ideas for the final draft of the lesson plan.
· Homework for stage 3: Group work – group 1 prepares the final draft of the lesson plan, groups 2 and 3 prepare the necessary teaching materials and aids.
Stage 3 The trainers
· check and discuss the final draft of the lesson plan and the teaching materials and aids with the trainees,
· together with the trainees they select two student-teachers who will teach the lesson in a real classroom.
Stage 4 At the secondary school
· the two student-teachers teach the 45 minute lesson. The remaining trainees and the trainers observe, take notes and video-record the lesson.
After the class:
· the student-teachers get immediate feedback from the learners (about 5 minutes),
· together with the other trainees and the trainers they discuss the course of the lesson (about 10 minutes).
Stage 5 The trainees and the trainers
· watch the video-recording,
· reflect on the teaching experiment.
The trainers
· evaluate and assess the student teachers using the material for student-teacher evaluation and assessment during the teaching practice.
Assignments
a) Assignments for teacher trainees
· What prior knowledge is required for solving the task?
· Consider different starting numbers. What different stages do the sequences eventually reach? How many different stages are there?
· Look for ways of using one sequence to complete the others.
· Try drawing a diagram to show how numbers are related.
· Can you predict in advance any number that will be lucky/unlucky?
· What sorts of numbers produce sequences that are identical except for the first number?
· Try some three and four digit numbers.
· What proportion of the numbers for 1 to 50 is lucky/unlucky?
· Are lucky numbers more often odd than even?
· Investigate adding the cubes of the digits of numbers.
· Consider the previous mathematical tasks from the teacher’s point of view.
· Discuss the first and third part of the proposal: What is the optimum student grouping?
· Would you extend teacher talk? How?
· What is the proportion between student and teacher work?
· What is the optimum timing for this activity? State variables.
· Consider task management aspects from the learners’ perspective, e.g. systematicity, the proportion of oral/written work, division of roles.
· Mathematics taught through a foreign language: Write a translation of the assignment.
b) Assignments for the pupils (presentation of the context)
· Make a list of numbers considered by your family and friends as lucky numbers stating a variety of reasons.
· Results of our investigations show that different numbers are considered lucky for different people. Somebody’s lucky number might be unlucky for somebody else.
· This, however, should not happen in mathematics. Let us define the lucky number as follows: “Choose a number. Square each of its digits and add the squares to get a second number. Square the digits of the second number and add the squares to get the third number. Continue this way to get a sequence. If the sequence reaches 1, the original number is called lucky. If not, it is called unlucky”.
· Find all lucky numbers from 1 to 99.
Piloting
a) In the training course
A priori analysis of the text
· Discussing possible mathematical solutions.
· Anticipating methodology problems.
Preparing the lesson [this stage was video recorded by one of the trainers]
· The trainers and trainees discuss in Czech how to best prepare the
microteaching of peers. They assign roles and prepare the first draft of lesson
plan.
![]() Video 1
Video 1
· Peer-team teaching in English: One stage of the proposed lesson is
taught by two student teachers, the remaining trainees play the roles of
pupils. One trainer takes notes on the blackboard for further discussion.
![]() Video 2
Video 2

Photo 1. Peer teaching
· Trainers and trainees analyse the teaching attempts in English based
on the notes on the blackboard. Comments and suggestions for the real classroom
are proposed. The aim of the lesson is set for both mathematics and English.
![]() Video 3
Video 3
· Mathematics – solving strategies.
· English as a foreign language – mathematical talk.
· Trainees divide into groups and decide who will prepare the final draft of the lesson plan and who will work on preparing the teaching materials (e.g. pictures, glossary of words) and they discuss the necessary aids.
b) In the classroom
The town of Kladno, lower secondary school, optional lesson, 8 pupils, 15 years of age, the classroom teacher, one of the teacher trainers, 45 minutes.
Teaching the lesson [this stage was video recorded by one of the trainers]
· The staffroom: Checking the lesson plan, materials, and aids.
![]() Video 4
Video 4

Photo 2. In the staffroom
· The classroom:
o
Introduction: The
teacher motivates the pupils in English: good luck vs. bad luck.
![]() Video 5
Video 5
o
The teacher presents visuals – six pictures.
Pupils are asked to describe, the teacher elicits responses from pupils.
![]() Video 6
Video 6

Photo 3. Using visuals
o
More information from pupils, unrelated to
pictures, the teacher writes on the blackboard: lucky/unlucky numbers.
![]() Video 7
Video 7
o
The teacher presents a problem: Is her date of
birth a lucky or an unlucky number?
![]() Video 8
Video 8
o
Listening comprehension: The teacher tells a
story about a kingdom – lucky numbers.
![]() Video 9
Video 9

Photo 4. Telling a story
o
The teacher introduces simple mathematical
language in English.
![]() Video 10
Video 10
o
Introduction of the procedure using 2 as the
starting number (see Photo 5).
![]() Video 11
Video 11

Photo 5. Switching into mathematics
(Example: 2 → 4
→ 16 → 37 → 58 → 89 → 145 → 42 → 20
→ 4)
o Controlled practice: The pupils and the teacher write on the blackboard (a similar problem: February, i.e. 2nd month, is it lucky or unlucky?).
o
Free practice: The pupils carry out an
individual pen and paper activity. The problem: “You proposed certain numbers
as lucky for your families and friends. Will they remain lucky if you apply our
procedure?” Feedback: Two pupils write on the blackboard.
![]() Video 12
Video 12
o
Further practice: individual work. The teacher
poses the following problem: Is your date of birth a lucky or unlucky number?
![]() Video 13
Video 13
o Revision of vocabulary in English: months. Further investigation linking to the mathematical topic: Is the pupils’ month of birth a lucky or unlucky number? The teacher elicits feedback: Individual pupils come to the front, write on the blackboard, and report back to the class.
o
The teacher summarizes the class with the pupils
using the table of numbers on the blackboard.
![]() Video 14
Video 14

Photo 6. Table for the summary of results
o The teacher concludes the lesson.
c) In the training course
A posteriori
analysis – reflecting on the lesson [this stage
was also video recorded by the trainer].
![]() Video 15
Video 15
The discussion was conducted in English and was fairly free. The items discussed were:
· lesson analysis;
· comments;
· critical remarks;
· suggestions for alternatives.
During the discussion, the class spontaneously switched into Czech because both parties found it easier to express their feelings about the lesson in the mother tongue.
It was concluded that the experiment was the real success. Following to that, as a final point of discussion, one of the trainees decided to use the same materials and the lesson plan in order to carry out the lesson in a different secondary school through a different foreign language – Spanish. Her teaching attempt was also video recorded, this time by one of the trainees.
Concluding remarks
Comparing and contrasting the two video recordings enabled to make the trainees aware of the following facts:
· The personality of the teacher plays an important role because the lesson based on the same lesson plan with the same teaching materials might develop in a different way due to the different teaching style.
· Team teaching is advantageous for both the teachers and the pupils.
· Different foreign language of instruction did not constitute any obstacle to learning.
Suggested reading
Bastow, B. et al. (1990) 40 Mathematical Investigations. The Mathematical Association of Western Australia.
Novotná, J., Kubínová, M. & Sýkora, V. (1998): Matematika s Betkou 3. Praha: Scientia.
Novotná, J. (2000). Objevujeme v matematice. Pracovní dílna. In: Dva dny s didaktikou matematiky 2000. Praha: Univerzita Karlova v Praze – Pedagogická fakulta, p. 49-53.
Novotná, J. & Hofmannová, M. (2000). CLIL and Mathematics Education. In: Rogerson, Alan. Mathematics for Living. The Mathematics Education Into the 21st Century Project. Amman, p. 226-230.
Pavesi, M., Bertocchi, D., Hofmannová, M. & Kazianka, M., on behalf of TIE-CLIL project (2001). Insegnare in una lingua straniera. General editor: Langé, G. Milan.
by Jaroslava Brincková, Iveta Dzúriková and Pavel Klenovčan
Pedagogical Faculty, Matej Bel University, Banská Bystrica, Slovak Republic
1. Mathematical topics for development
Arithmetic and application of algorithms for age 13–14
2. Description of the activity
Choose a number. Square each of its digits and add the squares to get a second number. Square the digits of the second number and add the squares to get the third number. Continue this way to get a sequence. If the sequence reaches 1, the original number is called lucky. If not, it is called unlucky. Distinguish notions to be happy and to have happiness. Investigate numbers in discussion club with the help of the Internet.
3. Aims
For trainers
· Guiding the trainees from theory to practice
· Providing instruction and feedback
For teacher trainees
· Mathematics: Problem solving, investigative mathematical procedures, generalisation.
· Methodology: Use methods of investigation in mathematics. Developing a lesson plan, peer teaching, classroom teaching.
For pupils
· Investigate numbers arranged by certain rules. Making problem solving more effective by discovering regularities.
· Practising skills of addition and multiplication of natural numbers.
· Investigate numbers in discussion club with the help of the Internet.
4. Assignments
See point 5 in the first piloting
In the assignments for teacher trainees the following task was added:
· Explain order of steps in solving problems in the scheme of Figure 1 below.
· Distinguish notions to be happy and to have happiness. Investigate numbers in discussion club with the help of the Internet.
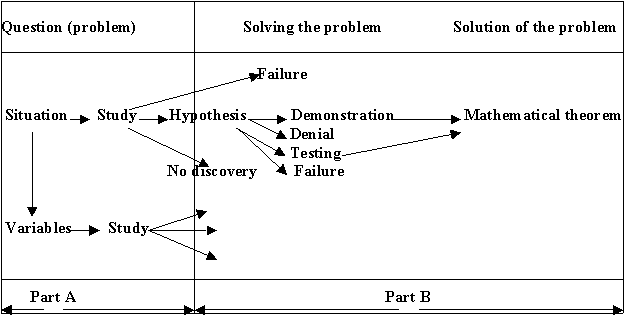
Figure 1. Problem solving procedure
5. Piloting
a) In the training course
Matej Bel University in Banská Bystrica, Pedagogical Faculty, Didactics of Mathematics course, Mathematics taught through English as a foreign language.
19 teacher trainees, 21- 22 years of age, 3 trainers, team teaching.
Time table: 45-minute training session, 5 successive weeks.
A priori analysis of the text
· Discussion about possible mathematical solutions.
· Preparing the lesson [video recorded]
· Discussion in Slovak [L1]: preparing the microteaching of peers.
Assigning roles, preparing the first draft of lesson plan:
![]() Video 1
Video 1
· Peer-team teaching in English [L2]: The teacher of English on lower level of 8-year grammar school has realised the lesson on topic My lucky number. The students have analysed video record with stress on mathematical communication in English.
· Students teach, the rest role play the pupils, one of the teacher trainers takes notes on the blackboard.
· Analysis of the mock lesson [L2] with the help of notes on the
blackboard. Comments and suggestions for the real classroom, etc. Setting the
dual aim of the lesson: Mathematics – solving strategies, English as a foreign
language – mathematical talk.
![]() Video 2
Video 2
· Preparing the lesson plan – stages [L2].
b) In the classroom
The town of Banská Bystrica, Evangelical 8-year grammar school, on lower level, optional lesson, 28 pupils, and 13–14 years of age, the classroom teacher, one of the teacher trainers, 45 minutes.
Teaching the lesson [video recorded]
· The staffroom: Checking lesson plan, materials, aids.
· The classroom:
o
Introduction – Teacher motivates the pupils [L2]:
good luck vs. bad luck.
![]() Video 3
Video 3
o Visuals – six pictures: description, teacher elicits responses from pupils.
o More info from pupils, unrelated to pictures, teacher on blackboard: Lucky/unlucky numbers.
o Teacher presents a problem: Is her date of birth a lucky or an unlucky number?
o Listening comprehension: Teacher tells a story about a kingdom – lucky numbers.
o Teacher introduces simple mathematical language [L2+L3].
o Introduction of the procedure.
o Controlled practice: pupils and teacher on blackboard. A similar problem: February, i.e. 2nd month, lucky or unlucky?
o Free practice: students – individual pen and paper activity. Problem: Are the numbers elicited in step 3 lucky or unlucky? Feedback: 2 students on blackboard.
o Further practice: individual work. Problem: Students’ date of birth – a lucky or unlucky number?
o Revision of vocabulary [L2]: months. Further investigation: students’ month of birth – a lucky or unlucky number? Feedback: individual students at the blackboard, report back to the class.
o Summarizing: rule discovery using the table of numbers on the blackboard.
o To be lucky – does it mean “to be happy”?
o Eligible problem: Investigate numbers in discussion club with the help of the Internet.
o Concluding the lesson.
c) In the training course
A posteriori analysis – reflecting on the lesson [video recorded]
Free discussion [L2]: lesson analysis, comments, critical remarks, suggestions for alternatives.
Free discussion [L1]: teacher trainees express their feelings about the lesson.
Suggested reading
Brincková, J (2002). 60 – alebo hry s číslami. In: Sborník příspěvků z mezinárodní konference na téma: “60 = 22·3·5?”, část 1. FP TUL Liberec 2002, s. 15-18, ISBN 80-7083-580-X.
Kopka, J. (2004). Výzkumný přístup v matematice. Ústí n. Labem: Acta Universitas Purkyniane.
Novotná, J., Kubínová, M. & Sýkora, V. (1998). Matematika s Betkou 3. Praha: Scientia.
Third piloting (at the University of Parma, Italy)
by Lucia Doretti
Department of Mathematics and Computer Sciences, University of Siena, Italy
The activity was coordinated by Daniela Medici and Maria Gabriella Rinaldi from the University di Parma, within SSIS (Specialisation School for Secondary Teaching) during classes devoted to the “Theory of didactical situations” and developed within three meetings:
First meeting (two hours): presentation of the problem situation to trainee teachers and successive work in groups for the analysis of the problem and identification of solving strategies. Discussion of proposals. Request, for the next meeting, of editing individually an a priori analysis in view of the classroom experimentation.
Second meeting (one hour): discussion on proposals emerged from a priori analyses and identification of classes for experimentation.
Third meeting (one hour): presentation of experimentations and discussion.
Notes and comments
For pupils from the classes
It was an experience that led them to look at natural numbers with different eyes, that is as “objects” with properties to be found and regularities to be studied. The activity, proposed as a game and a challenge, allowed pupils, working in small groups, to be directly engaged and raised interesting remarks to “fasten” the search for lucky numbers. Becoming aware of the problem situation stimulated pupils to search for lucky numbers with three or more figures and made them curious to get to a rule to find lucky numbers, they thought should necessarily exist. It was quite disappointing to come to know that such a rule is not known in mathematics, whereas they expected teachers to reveal it at some point. Pupils were led to reflect on the activity, the value of which lies exactly in the fact that they got autonomously, through discussion and exchanges, to new discoveries and “meaningful” reflections on the properties of numbers, although they did not have a traced path available. Almost all pupils, including those who were generally less motivated, participated in the activity, even though some were still puzzled about the usefulness of the work, since they “had not learned any new calculation rule”.
For trainee teachers
It was the chance to reflect on the fact that investigating the multiple features of natural numbers can not only be curiosity, fun and play but also constitute a first step towards mathematics as search and discovery.
Trainee teachers, facing the problem of searching for lucky numbers, lived the same experience as their pupils: in front of a new problem, they need to explore its mathematical aspects and seek suitable strategies. They realised how useful this phase is to design and manage the activity in the classroom.
Planning a classroom intervention first individually and then through collective discussion made all the trainees feel involved and helped those who materially managed the implementation of the teaching experiment, as confirmed by the a posteriori analysis. In telling the story of what happened in the classroom, the experimenters pointed out the importance of and difficulties in managing the first phase in which the pupils had to get to understand and correctly use the “definition” of a lucky number. Overall they viewed the experience as an interesting opportunity for “experiencing how an a-didactical situation captures pupils’ attention and stimulates their curiosity thus creating in the classroom conditions necessary to develop an interesting mathematical activity”.
For trainers
The activity fell into the “Theory of didactical situations” domain, as an example of a-didactical situation, and was considered interesting by trainee teachers. Everybody seemed to be engaged, due to collaborative work and collective discussions, since nobody, including the trainers, had a “recipe” or the “solution” to get to. Many remarks were made and work was carried out in a very “constructive” atmosphere.
One of the key issues in teacher education is a way how to set and maintain optimum balance between theory and practice, i.e. between the prospective teachers’ knowledge on the one hand and their practical professional skills on the other. Over the years, there has been a lot of discussion on this problem with a number of different educational models compared and contrasted, their results analyzed and evaluated. The ideal solution, however, has not yet been agreed upon or found.
All teacher trainees in mathematics who enrol at faculties of education or other teacher training institutions have attended mathematics courses at primary and secondary schools. They have gained not only more or less extensive and deep awareness of notions and mathematical competences, but also a very personal experience of being taught. Teacher’s prior experience can have significant influence on his/her ability of empathy as regards the cognitive processes of the pupils who often face the need to deal with new, often surprising notions, their properties and relations.
New educational materials put the stress on experimentation, data collecting, observation, rules discovery, generalizing, and hypotheses testing. Taking into account diversity of learning styles, such teaching strategies also promote individual approach towards the process of education.
The proposed and piloted activity called My Lucky Number is aimed at future teachers of mathematics attempting to link their mathematical knowledge and skills with the professional ability to teach the subject. As is shown in the three piloting events, for the teacher trainees it offers both the opportunity to simulate situations that can happen in the classroom, and a fair chance to reflect on their attitudes (conscious or non-conscious) towards mathematics and the way it is to be taught.
The original aim of the activity was to develop the pupils’ ability to investigate in mathematics and to make use of the found properties of mathematical objects for further discoveries of object properties. Three piloting events of the activity called My Lucky Number have shown at least some of the paths how to develop a simple mathematical situation for a variety of teaching aims and objectives. Let us now look at the main differences of the three events. The common features have become apparent through the description of individual events, and we have it that it is not necessary to go into any more detail. To point out the differences will certainly be more interesting for the readers.
In the first piloting that was carried out by the authors of the proposal, particular attention was paid to the possibility to implement the activity in the course preparing future teachers for Content and Language Integrated Learning (CLIL), i.e. teaching mathematics through English as a foreign language. That is the reason why strong emphasis is put on the development of pupils’ knowledge and skills both in general English and mathematical terminology. The preparatory stage in the teacher training course and also the real classroom teaching reflect this need. Individual preparatory steps aim at balancing the two main aims and creating meaningful links. The results of the secondary school piloting and follow-up discussions with the teacher trainees who participated in all the stages, testify to the fact that the activity made it possible for them to relate knowledge of both English and Mathematics (that they study at the university) with professional teaching skills necessary for the teaching of mathematics, English, but mainly for mathematics taught through English.
The second piloting was inspired by the originally designed scheme that was implemented in the first piloting, and drew on it significantly enriching it by two new ideas: reflecting on possible intersections in the solving procedure while dealing with (not only) mathematical problems, and using the Internet for mathematical discoveries. The proposed activity turned out to be a good example both in teacher training and school mathematics teaching. Especially the Internet discoveries seem to be a new and interesting experience for a number of prospective teachers who look for new paths in their professional development. Furthermore, it might become a strong aid in motivating pupils to an active approach towards learning.
The teaching/learning process can be characterized as a sequence of situations (natural or didactical) that result in modifications in the pupils’ behavior that are typical of getting new knowledge[1]. Peculiar to this process are the so called a-didactical situations where the teacher passes some of the responsibilities for the learning process onto his/her pupils. On the teacher’s part, it actually means delegating power, for the pupils it means gaining control. The pupils themselves, without the teacher’s direct intervention, are investigating and discovering, they are creating a model and checking its correctness and usefulness, or they are creating a different model that they consider more useful etc. Their activity is controlled only by the learning environment and their knowledge, not by the didactical activity of the teacher. Each pupil becomes responsible for getting the required results. The teacher’s task is to both facilitate such situations and institutionalize the information obtained by the pupils. The knowledge is further utilized and developed with the teacher’s help. The third piloting showed how to use the activity called My Lucky Number to prepare future teachers for designing a-didactical situations and their development. Even here the results were excellent.
Summarizing experiences from the above described piloting events, we can state that discovery strategies with all their subcomponents play a very important part in teacher education. The same is true when using discovery strategies with school learners. Our experiences confirm, that those students who get acquainted with such strategies during their studies, will be more open and prone to using them later in their own teaching. Moreover, they will not be afraid of difficulties they can encounter while working with pupils, they will be more open accept individual learning styles etc.
The proposed activity was by no means intended as the only one that can offer help in the above sense of the word. It is just one example of a certain type of useful procedures, and at the same time a challenging path to follow in teacher training. It is necessary to always bear in mind, that the main aim of such activities, tasks or assignments such as My Lucky Number, is not to elicit satisfactory answers to the teacher’s questions, but to assist the pupils to compare their prior knowledge and ideas with their own new discoveries, and also with the ideas and results of the others. The teachers’ task is not easy. They need to uncover principles of gaining knowledge in order to prepare such didactical situations that enable the pupils accept responsibilities for their own learning.
© LOSSTT-IN-MATH Project