Introduction

This theme combines three fundamental aspects of the teaching of mathematics in lower secondary school. The first one is defined in terms of its mathematical content: it involves proportionality, which constitutes one of the cores of pupils’ knowledge. The second one involves a didactic approach: combining a geometrical frame with a numerical context. The third one deals with the use of resources and the integration of new technologies. The combination of these three aspects forms an integral part of the overall scheme of training and is relevant to work with trainees on teaching practices in the classroom.

In the first place, this initiative was piloted by the two following partners: the IUFM of Créteil and the Skårup Seminarium; the external experiment was piloted by the University of Bari, in two grade 7 classes from lower secondary school (pupils aged 12-13).

 

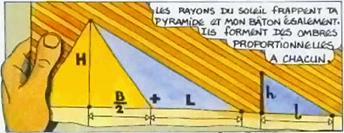
The legend about the measurement of the height of the Egyptian pyramid

 

PRESENTATION OF THE INITIATIVE IN THE IUFM OF CRETEIL

This initiative is an experiment carried out for the first time within the IUFM. From the whole range of training initiatives offered to maths trainee teachers in initial training, we have chosen for the project LOSSTT-IN-MATH the introduction to proportionality in geometry. This initiative demonstrates the trainers’ will to set up a training scheme which combines several modules while at the same time taking into account its future application of course for the project LOSSTT-IN-MATH, but also as a training tool within the IUFM itself.

Depending on the year, between 50 and 80 maths trainee teachers for lower and higher secondary levels (PLC2’s) go through the IUFM training in Créteil. It includes a 51 hour-long module of practices in the class of mathematics (module A). This module aims at accompanying the trainee teacher, in liaison with the educational adviser tutor, in his discovery of the teaching profession and at facilitating the build-up of his professional experience by providing him with teaching aids as well as pedagogic and didactic elements of reflection: official curriculum, the working out of modes of progression, preparation of sequences and sessions, evaluations, awareness of pupils’ diversity, mathematical contents, specific work in algebra or in geometry.

It also includes a module in geometry which aims at consolidating the foundation of acquisitions by trainee teachers, a foundation which will enable them to set up, control and manages pupils’ activities, on paper and/or on screen. The first three sessions are devoted to handling computer software programs in dynamic geometry (Geoplan-Geospace, Cabri); each trainee teacher is thus given the opportunity to construct figures, to make them evolve in a dynamic way, and to operate the specific software functionalities (transformation, search for locations, verification of properties, study of functions derived from a geometrical situation etc). The following two sessions allow the return to fundamental configurations of elementary geometry through tutorials, and the opening of ways of designing and setting-up activities of geometry in the classroom. The last two optional sessions, can provide opportunities to discover (or re-discover) in an elementary fashion three geometrical transformations: perspective, similarity and inversion.

As in any training initiative, the description and reflection involved will be carried out with a dual chronological approach: that of trainers towards trainees, followed by that of trainers interested in trainees’ practices and their effects upon pupils.

We will therefore specify our objectives and prior expectations concerning trainees, and then we will introduce the training initiative as it has been carried out this year, i.e. its development from beginning to end. This will be followed with a posteriori analysis, still at two levels, that of the session led by a trainee in the classroom and that more global of the initiative in its entirety. Finally, we will present some perspectives open to us as trainers at the IUFM of Créteil and as members of the project LOSSTT-IN-MATH.

A PRIORI ANALYSIS

The modes of the training initiative are worked out with work on practices in mind and not just making a speech and with the will to act upon both the cognitive and mediating components of the teaching profession.

To be more precise, our objectives in this initiative are:

·        To make IT technologies available to trainees as learning tools, in particular to make them aware of the benefit of using IT software in dynamic geometry as a special tool for a conjecture and for the discovery of the universality of a property.

·        To make trainees work on the design of a pupil’s worksheet where the instructions are not limited to the technical aspects of handling the software.

·        To make the trainees work individually on a detailed and real scenario. What are the pupils responsible for and what is the teacher responsible for? How to break the session down? What are the difficulties foreseen? Where to fit in the synthesis stages? Which institutionalisation (i.e. results and properties pupils have to get as knowledge according to curriculum)?

·        To make the trainees reflect collectively on their individual proposals in order to make them justify their choices.

·        To make the trainees deliver efficiently a session on which they will have worked collectively in order to make them realize that it is possible, that “it works”, to give them confidence and to encourage them to repeat this initiative (and other novel situations).

·        To examine how a novice teacher can make good use of IT resources to facilitate some learning processes for the pupils and establish a comparison with potential activities for pupils during a paper/pen activity.

·        To develop a pertinent use of IT in secondary education in accordance with the curricula.

DEVELOPMENT

The training initiative takes place in 4 stages:

·        During an IT module (making good use of software programs and instructions)

·        During a module A (work on scenarios)

·        During an effective delivery (sessions in the classroom)

·        Again in a module A (synthesis of experiences)

1^st stage

At the end of the first IT module devoted only to handling dynamic geometry software programs, the trainers ask the trainees to prepare an activity for 3^rd year pupils aimed at introducing proportionality in geometry. This preparation is done outside the training modules and consists in creating a scenario and designing a pupil’s worksheet. The trainees have the choice of two themes – introduction of cosine or introduction of proportionality in triangle, called in France “Thales’ theorem” – and two software programmes – Cabri or Geoplan-Geospace. The work is to be sent to the trainers of module A (classroom practices). The IT module is led by two trainers for a group of about fifteen trainees. As for module A it is run by two trainers for a group of between 20 and 25 trainees.

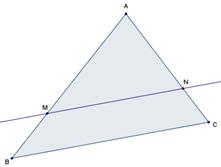
Picture 7. Thales’ theorem

According to the French official syllabus in force for 3^rd year pupils in 2004-2005[1]:

 

Table 4. Excerpt from the French syllabus

2^nd stage

The trainers involved with module A have received the trainees’ productions, have read them and annotated them. Most of the trainees have chosen the introduction to Thales’ theorem. The session is made of several periods.

It begins with the trainers making general comments mainly on two recurring observations. On the pupils’ worksheets, the trainees have not emphasized proportionality. Nearly every worksheet though contains the term “proportionality” in its title, the discovery of which being precisely the main issue of the session! In spite of this, the equalities of ratios are introduced very quickly without the possibility of demonstrating the proportionality of the lengths of the sides of the triangles. The scenarios are on the whole very basic, the different parts are only briefly described, and the teacher’s part is hardly noticeable. Moreover the formulation of the final conjecture does not stand out from the enunciation of a property.

Afterwards the trainees work in groups of 4 organized by the trainers according to their productions and also to their involvement in the previous modules (the trainers in so doing endeavour to create dynamic groups, with complementary personalities). Their task is to produce collectively a scenario and a pupil’s worksheet that will form the basis for a video projector presentation in the third part of the session.

One of the trainees will therefore then present to all the others the scenario re-worked within his group. Questions are then being asked by the other trainees forcing the presenter and his group to justify their choices, and alternatives appear. The trainers then give a synthesis of the session, bringing in their own comments. It is finally agreed to adopt one common scenario close to that presented. One of the trainees is responsible for drafting and finalizing the documents, scenario and pupil’s worksheet (see Appendix A). The aim of the session is to create a dynamic figure, so that pupils are able to formulate a conjecture.

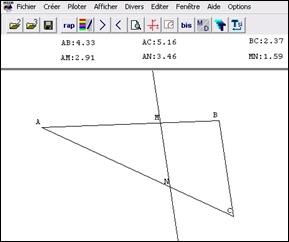
Picture 8. An example of the expected figure

3^rd stage

An effective delivery in all the classes taught by the trainees cannot take place as they do not all have a 3^rd year to teach. The filmed session takes place in the volunteer trainee’s classroom, without any institutional evaluation. During a previous meeting, immediately before the session, the trainee has introduced his class and presented his project to one of the trainers. In the same way he will after the session make some on the spot comments.

4^th stage

It is the return stage to module A. The trainee who delivered the session verbally shares with the others his feelings about being filmed and gives a short a posteriori analysis of the session. The trainers complete this analysis. The other trainees intervene to ask questions or to add to what has been said when they too have delivered the session in the classroom. No work however is being done with the trainees using a presentation of the video or an extract from it. There are two main reasons for this: firstly the structure of module A has been worked out before the start of the training and is very complex. Now the type of work undertaken on the introduction of proportionality in geometry and some of the modes of this specific training initiative were integrated during the course of the year. It was therefore difficult, bearing in mind the time constraints, to add a new element in the training. Secondly, video work is still underused in the training of maths PLC2’s at the IUFM of Créteil, and neither on the trainers’ side nor the trainees’ side did anybody feel quite ready to introduce this new tool as an integral component of training.

THE SESSION IN THE CLASSROOM [this stage was video recorded]

Presentation of the context

The IT session was carried out with a 3^rd year class from Edouard Herriot college, situated in Livry-Gargan, in the Eastern suburb of Paris. The class is made up of 23 pupils, sub-divided into 2 groups, one of 11 pupils, with whom a similar session has already taken place, and one of 12 pupils about to be observed; one pupil per computer.

The teacher is a trainee teacher in initial training at the IUFM of Créteil. According to him, managing the class does not involve any specific problem.

A rigorous follow-up of the pupils’ work has been put into place in the classroom on a daily basis and oral participation is taken into account during sessions.

The session is devoted to the discovery of Thales’ theorem at 3^rd year level. Geoplan has already been used by the teacher on screen and on the blackboard; the notion of pull-down menu has been introduced to the pupils on this occasion. To the teacher’s knowledge the pupils have never used Geoplan nor come into the computer room during the course of the year or in previous years, neither for maths nor for any other subject. The pupils are therefore discovering a new workspace.

The questions the teacher may a priori ask himself are the following:

·        How will the pupils react to the software program? Will they know how to use the pull down menu? Will they for example know how to find intersections of straight lines?

·        Which questions will they ask regarding the functionalities of the software program? (The teacher wonders in particular if the pupils will try to find out whether the calculation of ratios performed on the calculator could have been made with the help of the software program).

·        How will the pupils manage with their worksheet?

With regard to the conjecture, the teacher hopes that the pupils will tell him that the completed tables look like proportionality ones and that this statement will be derived from various examples. The theme of proportionality has been dealt with during the previous week, through 2^nd year revisions in a numerical or graphical frame: being able to recognize a situation of proportionality (in a table or in a graph), calculate a fourth proportional.

Approximately half an hour later the teacher plans to introduce the synthesis stage and to then have the pupils write in their exercise books, leaving them either in front of the screens or splitting them out at tables in the centre of the room. The beginning of the lesson is written at the back of the blackboard. He plans also to give them a generic drawing to stick on.

Development of the session

1^st period (16 min)

There is one computer per pupil. The software program Geoplan is opened at each workstation. The teacher quickly hands out the pupils’ worksheets. The pupils get to work quickly and make a reasonably easy start on the drawings. They have a marked tendency to watch their neighbours’ screen and to ask about each other’s respective progress. The teacher circulates in the room, from station to station.

The first difficulty arises when creating point N. Afterwards a second hesitation occurs over the number of decimals to be displayed for the lengths of the segments.

Finally the pupils get the display of the required six lengths, and then the teacher asks them to fill in a second table. They then undo the initial triangle in order to obtain new measurements. Video 1

2^nd period (17 min)

At this stage, the pupils remain puzzled, firstly as to the nature of the task (what does to conjecture mean?) and then on the task itself (what can they possibly conjecture?).

Then the teacher tries to put them on the right track by mentioning both the tables and what has been covered in class the previous week. The pupils begin by quoting Pythagoras’ theorem (we are doing geometry!), one of them mentions proportionality.

Then the pupils take their calculators to determine a possible coefficient of proportionality. But faced with the different results displayed on their calculators, they hesitate and find it difficult to formulate a conjecture in writing. They go back for more calculations on the first table. Video 2

The teacher approaches a pupil, and goes over the first calculations with him and then asks him to move on to the second table: The pupil seems a lot more satisfied with the quotients displayed since each of the 3 decimal figures starts with 1,70.

Picture 9. An example of pupils’ tables

The teacher goes back to the pupil, modifies the number of digits in the decimal part of the measurements displayed on the screen and asks him to take into account the new measurements and to perform new calculations.

A short discussion follows regarding the nature of the charts (proportionality or not), and the effect of the precision of the measurements.

The teacher asks the pupils to take their exercise books.

3^rd period (15 min)

The pupils organize themselves quickly, to be able to see the teacher, the chart, and to write at a table (some pupils sit at tables grouped in the centre of the room; others stay where they are turning round as necessary).

The teacher begins by making a verbal statement “It can be said that the lengths of the sides of the small triangle AMN appear proportional to the lengths of the sides of the big triangle ABC”. Video 3

Then he turns the board over, on which the enunciated sentence was already written and asks the pupils to copy it down on their exercise books.

Then he hands out a figure similar to those already studied by them, puts one on the board and certifies that “in such a configuration the chart is a proportionality one”.

The teacher then writes the following property (admitted): in a triangle ABC, if M is a point on side [AB], if N is a point on side [AC] and if the straight lines (MN) and (BC) are parallel, then the lengths of the sides of the triangle AMN are proportional to the lengths of the sides of the triangle ABC. The pupils in turn write down the property in their exercise books. Video 4

A POSTERIORI ANALYSIS OF THE SESSION IN THE CLASSROOM

The pupils are well managed; their involvement is noticeable and sustained.

The teacher has not included any intermediate synthesis stage: his interventions are always personalized; the difficulties encountered by the students are therefore repeatedly dealt with.

During the course of the first period (construction of the figure and display of lengths measurements), the use of the software program appears to have had a significant driving effect on pupils’ participation in the tasks required of them. The structure of Geoplan-Geospace has demonstrated the importance of designating geometrical objects: several pupils were thus confused when small letters used as capital letters were being rejected. Generally speaking, the necessity of defining the objects to be created has forced the pupils to pay more attention to the vocabulary used in geometry. The display of length measurements has also led the pupils into asking questions regarding the number of digits in the decimal part. However, there was no question from them regarding the unit of length used, nor on the choice of the number of digits to be displayed.

The transition from observation to conjecture was not spontaneously made by the pupils. Even after several verbal reminders from the teacher, the pupils did not mention any situation of proportionality. Only when the teacher referred insistently to other charts used the previous week, did one pupil mention proportionality. The “Topaze effect” is here clearly in evidence.

At this stage in the session, it is to be noted that the teacher has deliberately adopted a strategy consisting in the substitution of work on measurement charts with a calculator for work based on the observation of direct display of ratios by Geoplan-Geospace. The teacher gave two reasons to justify his choice: firstly he feared difficulties related to the pupils’ handling of the software, for whom this was the first session on Geoplan-Geospace, secondly, he took into account the preparation of the session done in training where the risk of obscuring the proportionality when working directly on ratios had been mentioned.

But the difficulties encountered by the pupils with their calculations, which resulted directly from his choice, had not been foreseen by the teacher. Indeed, the results displayed on the calculators are not equal. It is therefore natural that the pupils tend not to conjecture a situation of proportionality. The teacher handles “this didactic incident” by proposing to the pupils to increase the number of decimals in the display of the lengths measurements.

One would have thought when reading the pupil’s worksheet that the second table aimed at consolidating a belief derived from work on the first one: but the order in which the pupils’ activities actually run – filling in the tables, then calculations of the ratios for both tables, as opposed to work on one table, conjecture, then work on the second one – has come to contradict the original plan, and has therefore significantly weakened the experimental process.

Finally one can also wonder how the pupils really perceive proportionality, for the observed session can lead us to believe that it is the didactical representation often used in the classroom – the chart – that triggers the recognition of a mathematical situation. In other words, it obviously appears that here the notion of proportionality is not available, and that is the usual representation, supported by the teachers’ speech, which brings up the conjecture aimed at.

The last period of the session, the transition from conjecture to property, is rather moderately managed by the teacher: no work on proof, not even a speech on this very transition, on the reasons behind his choice. One can wonder about the effects generated by this situation on the pupils in terms of learning: Don’t the pupils in fact remain with geometry of perception (one sees that … it can be said that …)? Which status do pupils really attach to the property aimed at during the session: universal or relative to their drawing? Is it really always true or in some cases only, or “nearly true” sometimes?

By the end of the session, a number of variations can be envisaged:

·        Two pupils per workstation.

·        Make the pupils work on a drawing (with show of hands) before making them work on computers (lines, observations and first conjectures).

·        Have the ratios displayed by Geoplan-Geospace.

·        Set in the first chart the length of side [AB] of a triangle and the position of M on [AB], then move M on [AB].

·        Make the pupils start from situations corresponding to ratios 1/2 or 1/4.

A POSTERIORI ANALYSIS OF THE TRAINING INITIATIVE

This whole experiment is a source for new questioning, regarding the subject dealt with in the classroom on one hand and teacher training on the other hand.

Teachers in initial training (and the others too) are forced to follow official instructions. The analysis of the session carried out in the classroom and in particular the teacher’s choice to drop the display of ratios for the use of tables and a calculator raises the following question: Does the wording of Thales’ theorem as it appears currently in the syllabuses encourage work to be done on the ratios or on the aspect of proportionality in geometry, as will be the case with similar triangles in the 5^th year? The answer is not an institutional one since this double aspect appears in fact quite explicitly in any of the three columns, contents/skills/comments of the syllabus. It remains therefore for the trainer to make up his mind in view of the “good practices” aimed at by trainee teachers. Choosing to have the pupils work directly on the ratios has certainly the advantage of enabling them to arrive more easily at a conjecture, the equality of the ratios, but incurs the significant risk of obscuring the proportionality of the lengths. On the other hand, trying to make the pupils conjecture a situation of proportionality may seem more meaningful, but more difficult to achieve, with the risk of a diminished involvement from the pupils. It has to be stressed that in both cases, the work is carried out on the measurements, and not on the magnitudes.

In order to take into account both the double aspect mentioned above and the a posteriori analysis of the session, it seems therefore reasonable, and reading the new syllabuses seems to suggest it, to propose the following steps to trainee teachers:

·        To start with pen/paper work on simple cases.

·        To have the pupils conjecturing these specific cases in terms of “...times more…” “… times less …”

·        To translate this conjecture in the form of an equality of ratios.

·        To resort to computer software in dynamic geometry to reinforce this conjecture by using the display of ratios.

·        To enunciate the property aimed at, in the double version proposed by the syllabus, proportional lengths and equality of ratios.

CONCLUSION

Besides the training objectives defined in the first part of this presentation, work in training, based on the construction of a scenario of one identical session for all the trainees has been retained a priori for two main reasons:

·        It facilitates module work (before and after)

·        It encourages the study of the effects of teacher’s practices on pupils’ activities from one single prescribed task.

·        The reflection carried out during and after this work allows us to think that this effective training has indeed complied with the initial objectives and seems to confirm the relevance of this type of initiative at several levels:

·        The integration of TICE (IT) in trainees’ practices

·        The importance of the production of written scenarios and of their application

·        The diversity and depth of the exchanges between trainees/trainees and trainers/trainees

·        The emergence of a typical scenario, the validity of which, yet to be tested, would be justified by a good compromise between a high potential degree of appropriate use by the trainees and a satisfactory degree of effectiveness in the classroom (the first point being necessary for the second one to happen, but in no way sufficient).

However, the video work carried out with one trainee, does not guarantee in any way an impact on the other trainees. The problem of the evaluation of the knowledge acquired by the pupils in the filmed trainee teacher’s classroom and also that of the evaluation of the effect of such an initiative on the practices of the other trainees remain therefore on hold.

Suggested Reading

Alvez, Y., Le Yaouanq, M.-H., Carême, A., Chareyre, B., Cleirec, N., Gastin H., Guillemet, D. & Saint-Raymond C. (2005). Collection Math’x: Seconde, Première S, Terminale S. Editions Didier France.

Autour de Thalès (1995). Commission Inter IREM Premier Cycle.

Brousseau, G. (1995) Promenade avec THALES, entre la Maternelle et l'Université. In Autour de Thalès, IREM de Lyon Villeurbanne.

Hersant, M. (2005). La proportionnalité dans l'enseignement obligatoire en France, d'hier à aujourd'hui. Repères IREM N° 59, TOPIQUES éditions Metz

Robert, A. (2005). Quelles différences y a-t-il…? Exemples d’analyses didactiques d’exercices ou d’activités élèves (collège ou lycée). Bulletin APMEP 457, 226-238.

Web links

French Curricula

[http://eduscol.education.fr/D0048/LLPPRC01.htm] and

[http://www.cndp.fr/secondaire/mathematiques/]

A.I.D. (Association pour l'Innovation Didactique) C.R.E.E.M. (Centre de Recherche et d'Expérimentation pour l'Enseignement des Mathématiques)

[http://www.aid-creem.org/telechargement.html]

C.R.E.E.M. was a specialised centre within CNAM (Conservatoire National des Arts et Metiers) created in 1972. For more than 10 years C.R.E.E.M. was a privileged partner of the Ministry of National Education in the management of Lycees and Colleges, and later in that responsible for developing new technologies (DITEN, and then DISTNB). On 26^th February 2003, CREEM closed its doors for good. It has been replaced with the Association for didactical innovations

Geoplan/Geospace

[http://www.crdp-reims.fr/Ressources/lib/Titres-reseau.htm?produits/pdt118.htm]

Geoplan-Geoplace is windows-based mathematics software for use from primary school to university. Geoplan-Geospace is software for mathematical constructions that allows dynamic and interactive representations. It allows the user to define and manipulate numerical and geometrical objects in a plane or in space (points, straight lines, circles, spheres, solids, convex polyhedron, numbers, transformations, loci, curves, vectors, numerical functions, numerical sequences, prototypes, etc.). These creations and manipulations can be automated by adding new commands.

Cabri  [http://www.cabri.com/v2/pages/fr/index.php]

Cabri II Plus is a tool for the realisation of geometrical constructions, just as you would on a piece of paper with a pencil, ruler, compass, and rubber. The software brings a new dimension to these constructions: the figure and its elements can be freely manipulated by the user and the construction is immediately updated. The constructions can be integrated into documents (under Mac, Windows) or published on the Internet (Cabri.Java).

 

Aims

For trainees:

·        To develop a lesson plan involving a dynamic geometry programme.

·        To learn how to use information technology in teaching.

For pupils:

·        To learn how to use a software programme in dynamic geometry

·        To derive the connection between proportionality and similar triangles using a dynamic geometry programme.

Proposal

First the trainee teachers must learn to use the dynamic geometry programme. We use the programme Geometer, a Danish version of Geometer Sketchpad. Through exercises the students become familiar with the most common facilities of the programme within classic geometry.

After that, we look at the idea on which we want to focus: the connection between proportionality and similar triangles.

Definition: Two figures are similar, when one of them is an enlargement of the other.

The students know how to use the connection, but have not yet explored in depth the theorems that specifically apply to this idea.

After the lesson with the pupils we will take a closer look at these theorems, in order to prove and use them. Partly the theorem of multiplication around a point, and partly the idea of similar triangles and their properties:

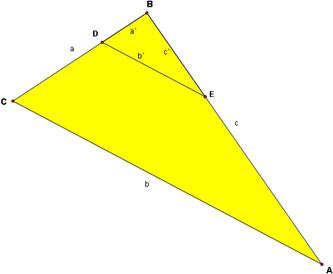
Triangle ABC has equal corresponding angles to triangle `A`B`C`.

Triangle ABC and triangle A`B`C` have corresponding angles that are equal.

The ratios between the corresponding sides of the two triangles are equal, i.e.

a'/a = b'/b = c'/c

Once the trainee teachers have become familiar with the Geometer program and the properties of similar triangles, their task is to then prepare a lesson for a (school) class. The aim of the task is to introduce them to the programme and to the properties of similar triangles.

The course which ends here is followed by an evaluation.

Later the trainees will have a study week in mathematics, during which the teacher trainer have planned two days of surveying about proportionality in geometry.

 

Picture 10. Illustrating proportionality

Instructions for the trainee teachers

There are about 25 trainee teachers at Skårup Seminarium. There is a wide age range and the gender distribution is about fifty/fifty.

Prior to starting this phase, the trainees have been practicing with the Geometer program as an introduction to its more general uses (operations, drawings, measurements and calculations). This was only meant as an exercise before the student teachers start to work on the preparation of the lesson for the pupils.

I gave the trainee teachers the following introduction:

“Your objectives for the next two weeks are to be able to make an introduction and create a document enabling the pupils to:

·        Draw triangles using the Geometer programme

·        Learn about proportionality and similar triangles by means of the dynamic geometry programme.

Trainee teachers work in groups and each group makes a proposal; the whole team then selects the best one.

This task should take one week (four lessons)”.

I have promised the class teacher in which this session will be piloted, to summarize this part. If needed, I will devote one additional lesson to the IT section. I will let the pupils use the mathematical knowledge they have previously acquired to carry out an actual survey, i.e. find the height of a tree using concrete measurements and then make calculations using the properties of similar triangles.

I would also very much like you to consider other real life situations where pupils can put into practice the concept of proportionality.

The trainees work with Geometer in the computer room on the connections with similar triangles. They work on establishing (property 1 and 2 above).

I suggest the trainees to do the following:

·        Draw a triangle ABC.

·        Enlarge or reduce the triangle by a given scale factor, using the instructions in the software (the result will be that the sides are increased/decreased by a given factor). You now have a new triangle ADE.

·        Measure the lengths of the sides of the two triangles ABC and ADE.

·        Find the relationship between the similar sides of the two triangles.

·        Measure the angles of the two triangles.

·        Let the points vary.

·        Let the ratio vary.

·        Derive the relationship between the sides and angles of similar triangles.

·        Measure the area of the two triangles and derive the relationship between the areas.

In the above exercise, we were varying the sides first and then the angles.

In the second method we can also do it the other way round, by first making the angles equal and then looking at the relationships between similar sides. What we do here is to start with parallel sides and then find that the triangles are proportional.

Do the following, using Geometer:

·        Draw a triangle ABC.

·        Draw a line inside the triangle. This line must be parallel to one of the sides. for example parallel to the side BC. Thus you have a new triangle ADE.

·        Measure the lengths of the sides.

·        Find the relationship between the similar sides of the two triangles.

·        You can then let the points and also the parallel line vary.

·        Derive what applies to the two triangles.

·        Measure the area of the two triangles and compare the relationship between areas to the relationship between the sides.

Here the angles are identical and you find that the lengths of the sides are in a fixed ratio. If you have any time left you can consider which practical examples could be incorporated.

The teacher trainees work on these points during two lessons.

The teacher trainer has chosen to let the whole group instruct the pupils as it would be good for the trainees both to prepare the lesson and to instruct the pupils.

As most of the pupils must sit alone or in pairs at the computer it will be best to have one of the trainee teachers at each computer.

The pupils have not yet used mathematics programmes so it will be beneficial if each one can have personal instruction.

Furthermore, the trainee teachers will get a good idea of what pupils can understand when they are later going to teach a whole class. I also hope that this will encourage trainee teachers to use IT in their maths lessons when they too later become teachers. A threshold may have been overcome, and they may be less reluctant to use mathematical software when they themselves become teachers.

The trainee teachers work in groups to make proposals for the pupils’ lesson. Video 1
Afterwards the whole group decides how to conduct the lesson. Video 2

Instructions for the pupils

One lesson is planned. The lesson will take place in the computer room at Skårup Seminarium.

The trainee teachers’ instructions for the pupils:

Lesson on Proportionality.

Start the program GEOMETER

Make 3 points; A, B, C

Connect the points to create a triangle

Measure the angles of the triangle

Measure the sides

Multiply by 2 from point A, i.e. you enlarge the lines from point A (2:1)

When the lines AB and AC are enlarged, the new points are renamed. Connect these two points to create a new triangle.

Measure the lengths of the sides and the angles of the new triangle

Can you see any similarities between the two triangles?

Which similarities do you see?

Can you formulate a theorem from your observations: if necessary, draw more triangles to verify your theorem?

Find the area of the two triangles (½ height * baseline)[3]

What is the relationship between these two areas?

Some trainees chose to work more independently, but most of them decided to use the printed instructions.

Progress of the trainee teachers’ lesson

Two lessons were used on self-test of the exercises as the basis for similarities.

The trainee teachers arrived at significantly different findings during these two lessons. It is an advantage for everybody to use IT, but some happily accept the media and use them while others are not very confident and are very slow; the biggest group however lies between these two extremities.

As before, the following two sessions were devoted to preparing the lesson for the pupils and again the whole group selected the best proposal.

Progress of the pupils’ lesson

There are twenty pupils from Øster Åby Friskole. They are about 14 years old.

One lesson is planned. This lesson takes place in the computer room at Skårup Seminarium. The pupils had little knowledge of proportionality and had never used mathematical software.

Some of the teacher training students had visited the class once before, during the lesson about mobile phones. The maths teacher of the class was present during the lesson, but only as an observer.

The pupils will work one by one or two by two and there is at least one trainee teacher to instruct them at each computer. Video 3

One of the trainee teachers welcomed the class briefly and introduced the lesson. Then the pupils started to work using Geometer. The trainee teacher’s introduction to the pupils can be seen under “Instruction for the pupils”.

Every group reached all the described points. The cooperation between the pupils and the teacher training trainees was good. Generally speaking the pupils were actively engaged on all points requiring the use of the geometer program and the teacher training students were good at helping them.

Some pupils succeeded in deriving general conclusions but the variation of their products was wide and because the trainees were anxious to get results, they led some pupils to the required conclusion. After the lesson the pupils handed in their work.

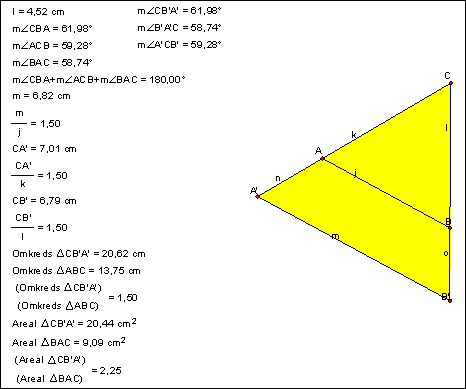
Picture 11. An example of one of the pupils’ drawings

Remark: As all calculations inside the programme are done directly from the measured values, it’s easy to make a direct comparison between the ratios without taking into account the position of the triangles in relation to each other.

evaluation

The feedback from the maths teacher of the class was that he believed it was a good lesson.

As basis for a dialogue I have created an evaluation scheme for the trainee teachers. The evaluation scheme is shown below with some answers already inserted.

 

Table 5. Evaluation scheme for the trainee teachers

Comments

The following session with the trainees is a theoretical connection between proportionality and similar triangles. Normally I would chose to prove the theorems about similar triangles and proportionality without any discovery activity, but in this case the proposal is to first experiment the properties through IT. The discussion will in this case be about the order of the activities: hypothesis and proof first or experimentation through IT. Personally I think we should vary. As for the trainees there is no unambiguous opinion. It seems that the younger ones would prefer the IT way while the others are more divided. An explanation for this may be that young trainees are often more familiar with computers.

It has been very fruitful, both for me as a trainer and for the trainees too, to be so directly involved in the planning of a lesson as well as in its implementation in the classroom.

Trainers are normally involved as advisers rather than participants during the trainees’ practical training: personally, thanks to the experience gained from this project, I will endeavour to change this. It has been very relevant to follow the whole process, from the trainees’ initial learning to the delivery in the classroom after preparation of the lesson. The trainees’ involvement has been considerable and their reflection sustained. The number of students actively engaged increases as they can see the direct relevance of what is being taught. It is highly motivating to be able to put immediately into practice what has been learnt.

I wish that the whole teacher training could be based on a regular interaction between theory and practice, so that maybe every month we were in dialogue about concrete training issues.

Follow up

The trainee teachers used similarity partly through practical measurements.

Examples of this could be: width of a river, experience how a woodman measures the height of trees, the slope of a roof for carpenters, interaction with Physics/Chemistry regarding distances in the universe and the determination of wavelengths, interaction with geography regarding scales and map reading.

Acknowledgement

Thanks to Øster Åby Free School, seventh class and their mathematics teacher, Brian M. Østergård.

Also thanks to my mathematics class 22.4 at Skårup Seminarium for their kindness.

Suggested reading

Hessing, S. (1987). Landmåling anvendt matematik og geografi. Forlaget Brøns ApS

Jensen, A. B. (2002). Manual til Geometer, L&R Uddannelse

Thygesen, H. (1998). Geometri med integration af informationsteknologi. Gyldendal undervisning.

Web links

The Geometer's Sketchpad [http://www.dynamicgeometry.com/]

Sketchpad is a dynamic construction and exploration tool that enables students to explore and understand mathematics in ways that are simply not possible with traditional tools or with other mathematics software programs. With Sketchpad, students can construct an object and then explore its mathematical properties by dragging the object with the mouse. All mathematical relationships are preserved, allowing students to examine an entire set of similar cases in a matter of seconds, leading them by natural course to generalizations. Sketchpad encourages a process of discovery in which students first visualize and analyse a problem and then make conjectures before attempting a proof.

 

First impressions

The initiatives carried out have shown a real interest, both from the trainees and from the pupils, in using geometry software, whether they had used this kind of software before or not. They have also revealed a necessity to ensure that teachers are properly trained to take into account the use of IT as a tool in the work they do with their pupils.

The idea was to enable trainees to use ICT in the classroom hoping that, in spite of possible material constraints, their first experience would prove fruitful enough to encourage them to continue. This objective has been achieved by most at Créteil and Skårup.

THE THIRD PILOTING

The theme of proportionality in geometry was tested in the training of trainee teachers at the University of Bari, Italy, by using the training initiatives carried out by the IUFM of Créteil and Skårup College of Education.

Below you will find an account of the experiment carried out by R.I. Ancona and M.A. Giovinazzi, two lower secondary school teachers.

Participating classes

Two year 7/8 classes from lower secondary school (pupils aged 12-13):

·       Scuola media statale “E. Fieramosca”, Barletta (Ba) composed of 23 pupils.

·       Scuola media statale “A. Manzoni”, Massafra (Ta) composed of 25 pupils.

Time allocation, instruments and materials

In the planning phase we envisaged at least 4/5 hours of laboratory-based activities (besides the classroom mathematics activity). In the actual implementation only 3 hours were devoted to laboratory-based activities.

Besides standard teaching materials the software “Geogebra” was used in class A and “Cabri II plus” in class B.

A priori analysis of the classes involved in the teaching project and planning of the activity

In class A there is a wide range of abilities; the working environment is collaborative, with a generally active participation by pupils in collective discussions. Pupils have good computer skills, but no previous experience in using dynamic mathematics software.

In class B the average level is higher (only two or three cases of little cognitive disadvantage can be highlighted). Pupils are expert Cabri users.

In both classes the theme “ratios and proportions” was introduced and dealt with in the weeks preceding the experiment.

The aims of the experiment were as follows:

·        monitoring in detail the effects of using an interactive educational software for teaching geometry;

·        verifying whether structuring suitable teaching worksheets allows us to monitor the intuitive reasoning stimulated by the use of this software.

Two stages related to the planning of the computer-based activity were envisaged:

·        introduction of the Geogebra software (this phase concerned only one of the two classes involved in the project, as the other class was already familiar with Cabri);

·        handing-out a practical worksheet related to the “Discovery of Thales’ Theorem”.

The type of questions to be included in the structured scheme varies according to their nature and their aims. We envisaged:

·        questions for reflection and testing on software-based constructions;

·        questions for reflection on the dynamic actions carried out;

·        questions on non-formalised hypothetical and spontaneous deductions;

·        check-questions on previous reasoning paths followed by pupils working in pairs.

The worksheet was handed out to pupils working in pairs.

Analysis and Reflections about the experiment

Use of an interactive software and comparison:

We did not record relevant difficulties in neither class concerning the proposed constructions. However their limited knowledge of Geogebra software did not allow pupils to use the software for calculating ratios between sides when they had to fill in a table related to the ratios between the sides of the two triangles. This led them to face the problem of approximate calculus, which in turn led them to find “close” rather than “equal” ratios most of the times (“we notice that the results of the divisions look alike”).

Both classes are used to working in pairs, especially in the computer lab. The “software expert” class showed a greater capacity for synthesis, whereas in the other class there was a clear need to “describe” the slightest observation in great detail. Discussions were good especially in pairs with a cognitive gap which was neither excessively high nor low.

Dynamic aspects of reasoning and reached conclusions

In the “expert” class the use of Cabri supported the construction of reasoning; it actually helped to test intuitive ideas pupils considered valid (for instance, the idea many had and quickly refuted, that “similarity” between triangles entails “unitary ratios between their sides”). In the case of a line cutting the triangle by a point D, though, the only highlighted aspect is a clear recognition of different triangles, without reflections about ratios between sides.

The use of Geogebra enabled pupils to control some geometrical aspects, but the outcome of operations with calculators brought about embarrassment. However the worksheet asked pupils to move point D many times and record the ratio; therefore in some cases the values were “almost completely” equal; moreover the worksheet focused again on ratios thus enacting a further phase of control of previous reasoning.

In the final phase, several pairs tend to check ratios when faced with the problem of another line intersecting the triangle by D.

Reflections on the whole experiment

Certainly this experiment tends to confirm that the use of dynamic geometry software adds value to the activity, making geometrical objects dynamic and confirming/reflecting/constructing mental images. Nevertheless, one cannot do without the simultaneous use of instruments that permit the checking of the intuitive thoughts that accompany this type of work. We believe that the worksheet was anyway a useful instrument not only to understand all the processes that were going on but also because completing it involved sharing ideas within pairs. What is certainly missing is a further phase of general “sharing” of ideas when designing a “classroom worksheet”.

Differences

However, some differences have emerged between the different partners regarding:

·        the choice of software and related activities (the software interfaces lead to the construction of figures in a certain way, inferring upon reasoning and learning processes);

·        the objective of the session in the classroom in terms of mathematical content;

·        the conditions required for implementation in the classroom;

·        the degree of integration of ICT into the curricula in various countries;

·        the importance given to ICT in teacher training;

·        how familiar the trainers are with ICT, how they use it both when teaching their pupils and when training trainee teachers.

The assessment of the session in the classroom confirms the benefits of using dynamic geometry software but reveals also that just knowing how to use them well technically is not sufficient.

The pupils have to be taught how to study the results they have arrived at and how to relate them to previously acquired knowledge if they are to draw, by themselves, pertinent conjectures from their observations.

Overall assessment of the training initiative with trainee teachers

The three training initiatives have highlighted four stages in the work carried out with the trainees:

·        use of geometry software;

·        design of a worksheet for pupils;

·        implementation in the classroom;

·        mutualisation and analysis of the experiments carried out.

It would appear that the benefits derived by the trainees from the training initiative are much greater when combining these four stages.

The design of a worksheet for pupils brings about one significant alternative: is it advantageous to draw up a worksheet for pupils common to all trainees, and if so at which stage (before or after the sessions delivered in the classroom)?

The issue in the preparation of any training session is whether it is more sensible to start from a document created by each trainee individually and to collectively develop it during the mutualisation phase, or to suggest a collective construction work towards one common document.

Choosing to create one worksheet common to all trainees before the session in the classroom results in a mutualisation phase easier to manage and places emphasis on the influence of classroom practices upon pupils’ activities. However this makes it potentially more difficult for each trainee to use the document individually.

On the other hand, creating individually a worksheet for pupils allows each trainee to prepare the whole of his/her session, thus facilitating their involvement and emphasizing their responsibility in the construction and the development of the session but does not lead them to such a comprehensive analysis; this is even more so in the case of a session involving the use of ICT.

The assumption is that professional training is enriched by the coexistence of all these different types of scenarios.

 

 

 

© LOSSTT-IN-MATH Project