Introduction

We consider it important that pre-service teachers master both mathematical problem solving and the choice and analysis of problems, together with the way of posing them in the classroom, so that pupils’ thinking processes may be better stimulated. The teacher must make several decisions about the organisation of their own teaching: these relate to the choice and systematisation of ‘good’ problems, the management of pupils’ personal solutions in the sharing phases (discussion), the possible ways for making these personal solutions evolve towards expert solutions, which are the main goal. In this context, a priori analysis becomes one of the professional tools helping teachers to formulate their choices and decisions (Charnay, 2003). The “Real world” problems proposal sits within a set of activities that stimulate work with problems starting from a suitable a priori analysis, in order to identify the mathematical concepts at stake and to determine whether, how and with what aims they can be used in teaching. The proposal provides an opportunity to select at least one of the suggested set of three problems “What a family!”[1], “Bizarre colouring”[2] and “The pursuit”[3], taken from the RMT – Rallye Mathématique Transalpin (Transalpine Mathematical Rally).

 

 

the Proposal

The “Real world” problems proposal is the first of the two enacted within the LOSSTT-in-MATH Project, in the Tuscan SSIS (Specialisation School for Secondary Teaching), Siena Centre.

There is a teaching module about problem solving within SSIS. In this module trainee teachers are led to discover the central role played by the problem solving activity in pupils’ mathematical education, through the experience of the Rallye Mathématique Transalpin (RMT). This is an international mathematical contest for both primary and secondary school classes, based on the solution of problems[4] (Jaquet, 1999), and some of the SSIS teacher trainers are directly involved in it, especially concerning aspects of educational research (Crociani et al., 2001; Crociani, Doretti, Salomone, in press). The choice of the RMT problems is due to their characteristics: to be relevant from the mathematical point of view and to allow connections with the mathematics program being taught in class, to motivate pupils and stimulate their involvement, to correspond with the various pupils’ stages in cognitive development, to offer the possibility of a range of strategies for resolution and opportunities for developing the children’s ways of representing the problem.

In the academic year 2004-05, the proposal involved first year SSIS students, Natural Sciences course, studying for a teaching qualification in Mathematics and Science in lower secondary school. The total number of trainee teachers was 15, none of which had a degree in Mathematics.

It was decided to work on the problem “What a family!” that requires logical-deductive abilities, more than specific mathematical knowledge. We think that such problems can find a good placing in the didactic practice, as they aim at the development of the pupils’ reasoning skills.

What a family!

Mr and Mrs Calculations have 5 children, whose ages are different even numbers. The sum of the three daughters’ ages is 30 years. The sum of the sons’ ages is 14 years. The sum of the ages of the two oldest children is 26. The sum of the two youngest children’s ages equals 10 years.

Indicate each child’s age and state explicitly whether it is a boy or a girl.

Explain your reasoning and indicate all possible answers.

The text of a problem is presented to trainee teachers, working in groups. They are invited to discuss and analyse the problem, making hypotheses about representations, strategies and reasoning paths pupils might use, together with possible difficulties and mistakes. Later the problem is presented in some classes, where pupils solve it working in groups and compare the procedures they followed with the present trainee teacher. The activity ends in the training course, with reports of classroom experiences and analysis of all the pupils’ written productions, commented upon by the trainee teachers in the light of the a priori analysis previously carried out.

Mathematical topics to be developed: Problem solving

Objectives

For trainers

·       To stimulate the use of teaching practices that view problem solving as playing a central role in the construction of mathematical knowledge.

·       To guide pre-service teachers in the a priori analysis of a problem and in the subsequent a posteriori analysis of pupils’ written productions.

·       To provide guidelines and feedback.

For pre-service teachers

·       To reflect on the problem solving activity and on the role it plays in pupils’ mathematical education.

·       To work with problems that not only require a mere application of known procedures but rather personal search, development of strategies, formulation of conjectures, checks and validation.

·       To analyse a priori a problem before it is used in the classroom in order to evaluate either the mathematical notions involved or those that should emerge, to foresee pupils’ strategies, modes of representation, difficulties, obstacles and possible mistakes.

·       To observe pupils when they are engaged in the solution of one problem, working in small groups.

·       To reflect on the fundamental role played by cooperative and collaborative activities in pupils’ social, affective and cognitive development.

·       To develop the capacity of analysing pupils productions not only with relation to the notions they used, difficulties they met or mistakes they made, but also for the different levels of sense, consistency and argumentation of the answers given.

·       To reflect on possible differences between predictions made through a priori analysis and results of the a posteriori analysis of pupils’ productions.

·       To use the information collected through both a priori and a posteriori analysis of problems to make hypotheses about specific teaching interventions in the classroom, if an actual need emerges.

For lower secondary school pupils

·       To gain expertise with problems that constitute a personal challenge and that stimulate both interest in and motivation for mathematical activity.

·       To develop a capacity of working in groups and to learn the basic rules of scientific debate: to express freely ideas, conjectures, reasoning paths; to have mutual exchanges, discuss, make decisions, check and validate …

·       To learn new procedures and representations from exchanges with others.

·       To develop metacognitive capacities through a reflection on thinking processes that guided the solving process and that allow for producing a justification of the answer and the reason for choosing that particular path.

·       To stimulate the use of hypothetical-deductive reasoning.

Description of the activity

The activity developed along three phases. The first and the third phase, each lasting 5 hours, involved the 15 first year students of the SSIS, Mathematical and Experimental Sciences specialisation; the second phase, lasting 2 hours was carried out in lower secondary school and was managed by two of the SSIS students.

Phase 1 (in the training course)

·       Trainers discuss with pre-service teachers about the meaning of the term problem, about the different types of problems and their use in teaching.

·       Pre-service teachers, working in small groups, receive the text of a problem taken from the TMR, solve it and carry out an a priori analysis on the basis of given tasks.

·       Each group presents and comments upon their work to other groups and both the solving procedures and a priori analysis carried out are discussed

·       A shared a priori analysis of the problem is written down.

·       They plan an intervention in the classroom in which pupils are expected to work in small groups on the problem.

·       Two trainee teachers are chosen and both of them will have to present, manage the activity in a class and collect materials produced by pupils.

Phase 2 (in secondary school)

The trainee teacher actually present in the classroom:

·       proposes and motivates the activity for pupils, who work in small groups

·       observes the work of one of the groups during all phases of the problem solution

·       manages the final discussion about solutions produced by the different groups

·       collects pupils’ written productions

Phase 3 (in the training course)

·       The two teacher-experimenters describe their experience in the classroom.

·       Pre-service teachers, divided in small groups, analyse all the pupils’ productions collected and write down their remarks.

·       Analyses of pupils’ productions are collectively discussed and they are compared with the a priori analysis of the problem.

·       Trainers and trainee teachers reflect upon and discuss possible didactical interventions that may help pupils to become aware of the mistakes they have made and overcome their difficulties.

Tasks

a) Tasks for trainee teachers

·       Which features of the problem can be highlighted, in comparison to classical textbook problems?

·       What are the mathematical contents at stake?

·       In which classes can the problem be posed?

·       What mathematical notions might be mobilised in pupils?

·       Which representation modes might be enacted?

·       What strategies might be used?

·       Will pupils be able to avail themselves of criteria to know whether they answered correctly or not?

·       What might be pupils’ difficulties and possible mistakes?

·       Plan a classroom intervention on a problem solving activity centred on the problem analysed, commenting upon the intervention a posteriori and proposing possible changes.

·       Compare and comment on the solving procedures produced by pupils, and on how they were justified

·       What type of didactical interventions might be designed to help pupils who met difficulties or produced wrong procedures?

b) Tasks for pupils

·       Separate into small groups and carefully read the text of the problem.

·       Exchange ideas and collaborate within the group.

·       Understand both information and requests included in the text of the problem, choose a representation for the situation and identify a possible solving strategy.

·       Check both choices made and results obtained.

·       Reflect on the path followed and write down their reasoning.

·       Exchange ideas and discuss collectively both procedures and representations used.

Piloting

a) In the training course

During the first hour, trainers discussed with pre-service teachers about the meaning of the term problem, on the different types of problems (problems for applications, problems to construct new knowledge, problems for the pleasure of searching and finding) and on their different possible uses in the teaching process.

After that we proposed the problem “What a family!”. Trainee teachers worked in groups of two or three elements. Each group received the text of the problem together with the tasks of solving it and answering some questions in writing. These questions aimed at collecting information about mathematical knowledge, modes of representations, reasoning, strategies, difficulties and mistakes pupils were likely to encounter.

Trainers’ aim was to lead trainees to reflect upon the important role played by an a priori analysis of the problem in view of better evaluating its didactical potential and possible uses in the classroom.

Each group was allocated one and a half hours to consider the problem, solve it and report on the solving procedure(s) they found on an overhead projector and complete their a priori analysis.

Various groups initially tried to solve the problem using algebraic tools, by setting up a system of equations. “Expert” processes were privileged as they were more familiar to pre-service teachers, although they were not suitable for managing the problem situation and in any case not generally usable in lower secondary school classes. Only after going back to a careful reading of the text could the groups unblock the situation and go ahead with hypothetical-deductive or combinatory reasoning starting from conditions provided in the text itself. Many were puzzled by the explicit request to indicate “all the possible answers”, implicitly pointing to the existence of more solutions. Only one group was able to find the three possible correct answers, while other groups provided one or two answers.

The preliminary work of a priori analysis of the problem was carried out quickly and with synthetic answers by all groups. The general impression was that trainees did not acknowledge this activity as important, as compared to the solution of the problem to which they devoted all their energies. Someone also underlined their difficulties in answering some questions and in predicting pupils’ behaviours.

The subsequent phase, lasting about one and a half hours, was devoted to sharing reflections and to a collective discussion. One member for each group illustrated the whole group work. Discussion centred on the different modalities used to solve the problem, on the incompleteness of reasoning paths that did not lead to finding all solutions and led to the identification of other different procedures. Trainees particularly highlighted the educational value of posing problems that have more than one solution, as opposed to the widely used model of problem necessarily having a unique solution.

The debate that followed led trainees to think about their a priori analyses and to reformulate a shared one that took into consideration what emerged in the collective discussion. This analysis is reported below.

Shared a priori analysis of the problem

Which conceptual domains are encountered by the problem?

Arithmetic – Logic – Combinatorics

In which class or classes may the problem be posed ?

Grades 7 and 8

Are there remarks that can be made about the text? If so, specify them and indicate possible changes.

The text is clear because it is broken into simple sentences.

It should be read slowly and carefully because it contains many conditions.

What pieces of mathematical knowledge can pupils enact or consolidate? Which possible new pieces of knowledge might be required?

Capacity of managing many conditions simultaneously.

Capacity of developing hypothetical-deductive reasoning.

Combinatory capacities (identifying all pairs and triads of even numbers that add up to a given value).

What type of representations, procedures or strategies might pupils use, taking into account the background knowledge they are supposed to have?

To express data through symbols and schemes so that they may be better visualised and easily checked.

We believe that procedures are based either on hypothetical-deductive or combinatory reasoning (analogous to those found by trainees)[5]

What difficulties might pupils meet and/or what type of mistakes might they make?

Forgetting some conditions because there are many to be taken under control at the same time.

Stopping at the first solution they find, or, if they guess that there are more, stopping at the second one, without checking for other possibilities.

Using algebraic procedures inappropriately [as trainees themselves did].

Highlight some educational values of the problem at stake.

The problem has more solutions and suits group-work, because it favours collaboration, exchanges and discussion among individuals.

Teachers and trainers then devoted one hour to prepare an intervention in the classroom, in which pupils were supposed to work on the problems organised either in pairs or in small groups, in order to favour both exchanges and discussion and to provide trainees with a certain number of written productions about the same problem.

The trainee teacher present in the classroom in the problem solving phase was supposed to observe pupils’ work: for this reason it was agreed that they focused on one group only and took notes of the procedures they followed in the different phases.

An observation sheet, reported below, was prepared for this type of activity, with some questions that could guide observation.

Observation of the pupil’s work

Phase of reading and understanding the problem

Who is reading? Is there any discussion during the reading phase? How long does the reading and understanding phase last? Are there pupils who participate actively and express their point of view? Is there a leader in the group?

Phase of solution

When it comes to the solution of the problem does the group hold together or break up? Are there exchanges in this phase of research? What kind of exchanges? Are there pupils who do not participate?

Phase of validation and control of found answers

Are solution(s) discussed within the group? How? Is there a control on the process? How do they come to a decision about the answer to be given? Is there still a leader in the group?

Phase of solution editing

How and why do they choose a pupil for editing the solution? Do those who are not writing control the process?

b) In the classroom

Two trainee teachers were involved in presenting the problem in two grade 7 classes, one with eighteen and the other with twenty pupils, aged 12-13. Each trainee was interacting with the pupils for the first time. During the activity, lasting overall about two hours, the class teacher was always present.

In order to motivate pupils trainees presented the problem as a mathematical game and a challenge for the class, inviting them to organise themselves into small groups. Each group was supposed to read the problem carefully, discuss it, solve it through a shared strategy and explain in writing the reasoning followed, being allocated 50 minutes. Work produced by each group would have been collectively discussed and commented upon in order to decide who met the challenge. While pupils were working, the trainee teacher present in the classroom focused on one group and observed and collected information about their way of going about the various phases of the problem solving activity. For this aim, specially designed questions were used.

The activity in class ended with a discussion on the different procedures used by the various groups and on the justifications produced. This led pupils to make explicit judgements on the efficacy and/or suitability of these procedures. At the end of the activity pupils’ written productions were collected to be later discussed and commented upon in the training course.

c) In the training course

The activity, globally lasting about five hours, was carried out again with the whole group of trainees. Those who went into the classroom told the story of their experiences to the group. Video 1

These stories brought to light different modalities of interaction within the two groups observed, which influenced the work and its success. They later reflected upon the importance of developing in pupils the capacity of working in groups, which involves being able to exchange ideas, to give one’s own contribution and accept those of others. It was also noted that this capacity is difficult to acquire, especially if it is not appropriately stimulated and regularly used.

After that the trainees again organised themselves into groups, were given the written productions of the problem collected in the classes. Each group examined pupils’ work with the task of writing down information about understanding of the problem, strategies adopted, mistakes made and difficulties met, but also on the explanations provided (for instance distinguishing between a complete and fully justified answer and a simple verification of the result found).

The subsequent phase involved sharing work, with the single groups presenting their own remarks and discussing them with others. In this phase, pre-service teachers participated in a particularly active and interested way. The a priori analysis and discussion of the problem was acknowledged to have fostered a more careful a posteriori analysis of the protocols: trainees stated they were led to put themselves in pupils’ shoes and try to interpret both their “way of reasoning” and their difficulties.

The concluding part was a synthesis of the remarks emerged throughout the activity.

Conclusions

The experimented practice forced trainee teachers to manage a mathematical problem solving activity on a “real” problem to be posed to a class.

The starting point was requiring them not to accept the problem uncritically but rather to try and evaluate a priori difficulties that pupils might have met in tackling it, to define what notions, representations and procedures were involved and predict pupils’ possible difficulties and mistakes.

We noticed that trainees moved from an initial perplexity and underestimation of the work requested to a progressively acquired awareness of its validity, especially when pupils’ written productions were analysed and discussed.

In the same way, they highlighted the importance of choosing to make pupils work in the classroom in small groups, in order to exploit the stimulus that a peer-to-peer exchange can offer to a discussion, and to a comparison and to exchanges of ideas and therefore to personal growth.

During the activity some trainees proposed to try and change some of the variables in the problem (numerical data, tasks, context,…) and study the effects of such changes on the problem and consequently on the possibility of using it. This idea was considered as an interesting route for developing this work.

Suggested reading

Bertazzoni, B. and Marchini, C. (2005). Improving classroom environment by problem solving. In Novotna, J. (Ed.), International Symposium on Elementary Maths Teaching, SEMT ‘05, August 2005, 78-86

Charnay, R. (2003). L’analyse a priori, un outil pour l’enseignant. In Grugnetti L., Jaquet F., Medici D., Polo M., Rinaldi M.G. (Eds). Actes des journées d’étude sur le Rally Mathématique Transalpin, RMT: potentialités pour la classe et la formation, ARMT, Dip. di Mat. Università di Parma, Dip. di Mat. Università di Cagliari, 199-213

Crociani, C. – Doretti, L. - Salomone L. (2006). Riflettere insieme agli insegnanti sul lavoro in classe con problemi del RMT: resoconto di un’esperienza. In Battisti R., Charnay R., Grugnetti L., Jaquet F. (Eds), RMT: des problèmes à la pratique de la classe, ARMT, IPRASE Trentino, IUFM de Lyon – Centre de Bourg-en-Bresse, 135-150

Crociani, C., Doretti, L. & Salomone, L. (in press). Riflettere insieme agli insegnanti sul lavoro in classe con problemi del RMT: resoconto di un’esperienza. In Battisti R., Grugnetti L., Jaquet, F. (Eds), RMT: des problèmes à la pratique de la classe, ARMT, IPRASE Trentin, IUFM de Bourg-en-Bresse

Grugnetti, L. and Jaquet, F. (2005). A mathematical competition as a problem solving and a mathematical education experience. Journal of Mathematical Behavior 24, 373-384

Grugnetti, L. and Jaquet, F. (in press). D’un concours de mathématiques à la formation des maîtres. Rencontre COPIRELEM, Strasbourg, Mai-Juin 2005

Jaquet, F. (1999). Présentation du Rallye Mathématique Transalpin. In Grugnetti L., Jaquet, F. (Eds.), RMT: Le Rallye mathématique transalpin. Quels profits pour la didactique? Dip. di Mat. Università di Parma, IRDP di Neuchâtel, 16-20

Medici, D. and Rinaldi, M.G. (2003). A teaching resource for teacher training. CERME 3, in [http://www.dm.unipi.it/~didattica/CERME3/draft/proceedings_draft/]

Web links

Transalpine Mathematical Rally           
[http://www.irdp.ch/rmt/]
[http://www.math.unipr.it/~rivista/RALLY/home.html]

 

 

For the purposes of piloting LOSSTT-IN-MATH proposals, we selected such units that seemed to be compatible with our Content and Language Integrating Learning (CLIL) course content. The activity “Real World” Problems was selected from the set of proposals available within the project. We believe that word problems in general are more prone to the approach adopted in Prague, i.e. teaching mathematical content through a foreign language. The final selection was Czech students’ choice. The title is Bizarre Colouring.

Proposal implementation

Title: Bizarre colouring

Original text:

Maxime is filling in a square grid. In each line, the rule of colouring is different:

 

 

He has already filled correctly the first 15 columns. He states that the columns 1, 9 and 13 are fully filled. He continues with column 16.

Will column 83 be fully filled? And what about column 265?

Explain how you have found the solution.

Mathematical topics for development:

Solving word problems. Patterns. Combining arithmetic, algebra, geometry, combinatorics, etc.

Aims

For trainers

·       Guiding the trainees from theory to practice.

·       Guiding the trainees to adapt the lesson plan and teaching materials to the pupils’ age and level.

·       Providing instructions and feedback.

For trainees

·       Mathematics: Word problem solving, generalisation.

·       Methodology: Material development to enhance pupils’ motivation.

·       Adapting a lesson plan.

·       Trying and testing the student made materials that combine English and mathematics.

·       Peer teaching.

·       Classroom teaching.

For secondary school pupils

·       Experiencing the teaching of mathematical content through the medium of English language.

·       Building awareness of an imaginative and creative effort in the search of solution.

·        Making conjectures, taking decisions, checking and verifying the results.

Piloting

a) In the training course

Charles University in Prague, Faculty of Education, an optional CLIL course, Mathematics taught through English as a foreign language.

10 teacher trainees, 22-25 years of age, 2 trainers, team teaching

Time table: 45-minute training session, 4 successive weeks

A priori analysis of the text

·       Discussing the proposed problems from the perspective of possible mathematical solutions and language of the assignment.

·       Choosing one of the three proposed problems as the basic problem for further elaboration (Bizarre colouring).

Preparing the lesson

·       The trainers and trainees discuss in Czech how to best prepare the microteaching of peers. They assign roles and prepare the first draft of lesson plan.

·       Peer-team teaching in English [this stage was video recorded by one trainer]: One stage of the proposed lesson is taught by two student teachers, the remaining trainees play the roles of pupils. One trainer takes notes on the blackboard for further discussion.

·       Reflecting and analyzing (in English) the training lesson: Trainees present critical remarks both to the wording of the problem and the execution of the lesson plan. The necessity to change the assignment in order to fit real life is emphasized. The trainees volunteer to prepare a new teaching material that would better correspond with the pupils’ age and interests. For the result see Appendix A.

b) In the classroom

Secondary school in Prague, one 45-minute lesson taught instead of an English class, 14 pupils, 15-16 years of age, a teacher of mathematics, an English teacher, two teacher trainers, a teacher trainee – observer

Teaching the lesson [This stage was video recorded by one of the trainers]

·       Introduction: The teachers organize an ice-breaking activity “Names scrabble”, introducing each other. Teaching material: Square grid. Video 1

·       Revision of mathematical terminology necessary for task completion. Video 2

·       Teachers assign the original (RMT) version. Pupils solve it either individually or in pairs. Video 3

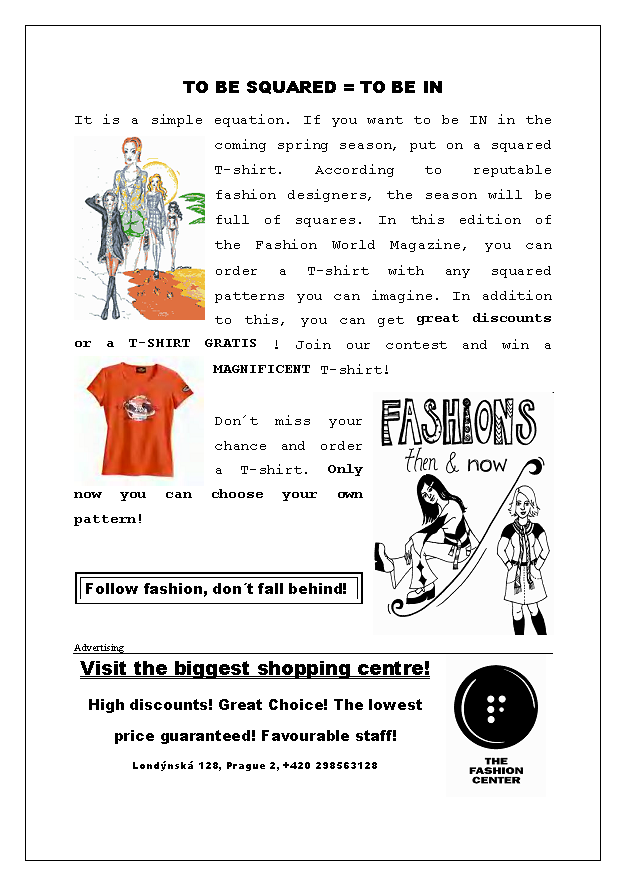
·       Teachers change the focus of the lesson (from mathematics to English): They introduce Maxime, the character from the “Fashion World Magazine”. They distribute the “Fashion World Magazine”.

·       English language: Teachers check pupils’ listening and reading comprehension.

·       Mathematics assignment: Pupils answer the questions from “Fashion World Magazine”. Video 4

·       Solutions are checked with the whole class. Video 5

·       The teachers conclude the lesson. Video 6

c) In the training course

A posteriori analysis – reflecting on the lesson

The discussion was conducted in English. The items were:

·       lesson analysis

·       comments

·       critical remarks

·       suggestions for alternatives.

Suggested reading

Harmer, J. (1989). The Practice of English Language Teaching. Longman

Novotná, J. (1999). Do students of the 3^rd to 6^th grades use the everyday life schemes when solving word problems? In Hejný, Milan and Novotná, Jarmila. Proceedings SEMT 99. Praha: Univerzita Karlova v Praze, Pedagogická fakulta, 1999. p. 159-163. ISBN 80-86039-86-2.

Pavesi, M., Bertocchi, D., Hofmannová, M., Kazianka, M., on behalf of TIE-CLIL project (2001). Insegnare in una lingua straniera. General editor: Langé, G.

 

 

The theme of the proposal, focused at problems and problem-solving, for its complexity and numerous implications is fit for being dealt with in a variety of ways, depending on the point of view that we want to adopt to make it emerge in the didactic practice and in teacher training.

The diversity of the viewpoints can be clearly seen in the report from the piloting by the different partners. For the partner who presented the proposal, the main focus was on the didactic situation. In the activity with the teacher trainees, who worked on the What a family! problem, the central role was assigned to the a priori problem analysis, completed by the subsequent a posteriori analysis of the pupils’ written production. Teacher trainees had to analyze the problem before proposing it to the classes; and to confirm, to correct or to disprove, by the comparison of the experimental data, what they had foreseen a priori. The general lines of the activity and the way it was implemented let the a priori be perceived as one of the professional tools that can help the teacher and orientate him/her in the choices to be made and the decisions to be taken.

For the co-piloting partners the most important aspect in the proposal was the verbalization. In fact, the nature itself of the Content and Language Integrated Learning (CLIL) training course, within which the activity was implemented, required from the teacher trainees to deal with mathematical contents by the use of English as a foreign language. It was therefore necessary to make available a didactic situation that fitted for a suitable formulation in linguistic terms, both to motivate the learners to the use of English and to stimulate them on the mathematical side. During the preparation of the lesson the teacher trainees worked on the text of the Bizarre colouring problem, suitably modifying its context and assignments. The new version differs from the original one for fantasy and originality: the idea of a contest based on a mathematical quiz to get great discounts or a T-shirt free of charge makes the problematic situation concrete, making it closer to a situation from the real life. Trainers thus obtain good material to stimulate and enrich learners both on the linguistic side (by the use of English) and the mathematical side (in this version the concept of least common multiple is involved).

As regards the non-partner institution (the Catholic University in Ružomberok, Slovak Republic), the study of the proposal represented the opportunity to tackle, with the trainees, the issue of the complexity of the text of a mathematical problem. They started considering that a problematic situation can be seen as a structure that contains several inter-related parameters. The knowledge of what has been given has an effect on what has to be found and can make the solving activity differently complicate, at mathematical level, for the learners that have to develop it. In the implemented activity trainees were led to create a scaled series of word problems and to evaluate the difficulty level of the solving process, before piloting this kind of material in the classrooms, with the pupils.

 

 

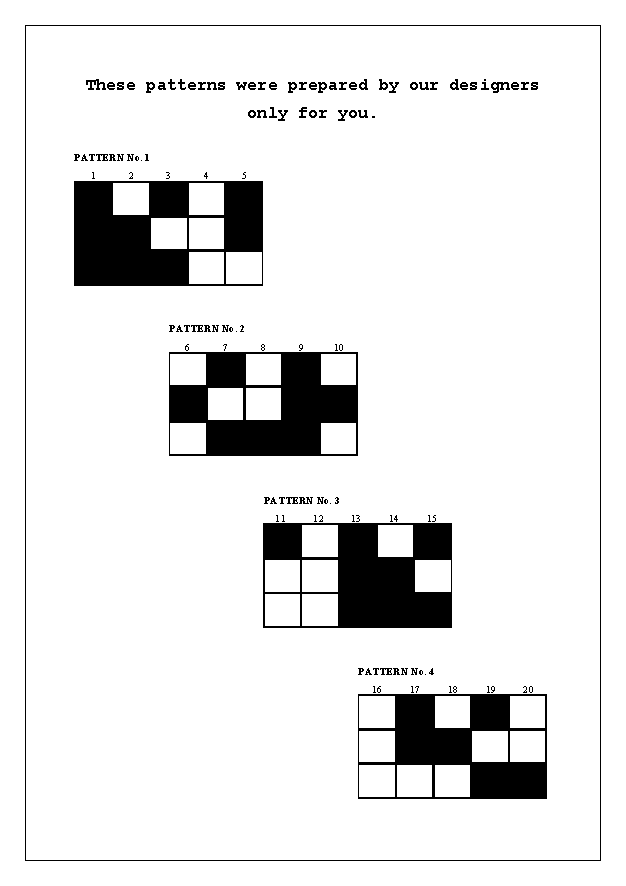
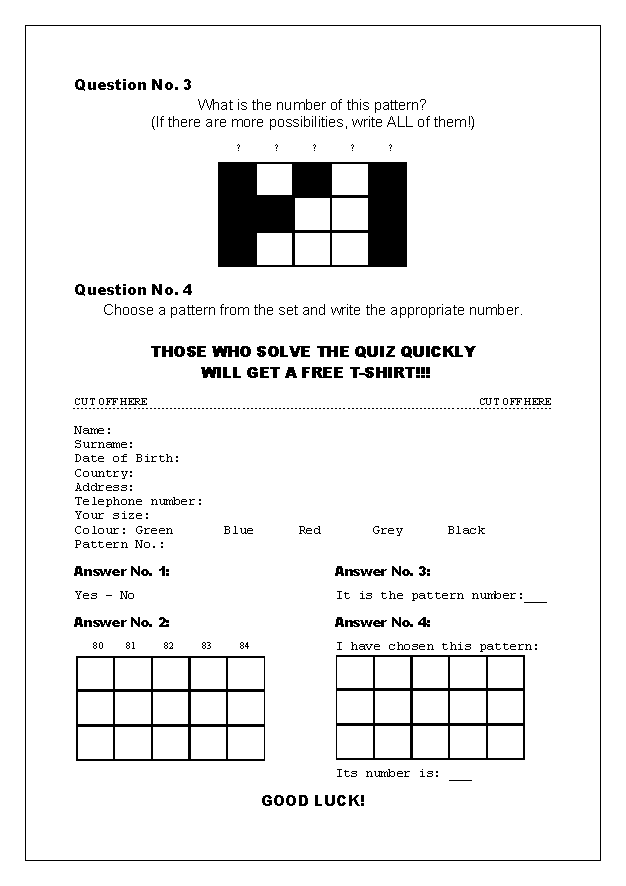
© LOSSTT-IN-MATH Project