Introduction

Learning is the outcome of an activity and it is also developed via activity. Among activities which pupils perform quite often are mathematical games. If such games are performed according to the rules satisfying certain didactical goals, they are called didactical games in the educational process. These didactical games include various geometrical puzzles, among them an old Chinese puzzle called Tangram. From the educational point of view, Tangram assists in teaching geometry via developing:

1.     geometrical knowledge,

2.     reasoning,

3.     geometrical imagination.

Geometrical imagination is ability to sense:

·         geometrical shapes,

·         their size and position in space,

·         a given shape in different space positions,

·         changes of shapes in their size, structure, etc.,

·         a shape in space according to its plane projection and a word description,

·         a plane representation of a given shape in space.

 

 

In teaching geometry, various activities can be carried out which strengthen the geometrical imagination by modelling via a paper-Tangram in E₂ (plane) or via a kit-Tangram in E₃ (space).

Picture 1. Tangram tiles

Rules for using Tangram

·       All seven parts of Tangram must be used when creating any shape.

·       No parts of Tangram can overlap.

·       All parts can be used upside down if needed.

 

In teaching geometry, parts of a Tangram-kit can essentially be used in two ways:

·       To model a given prescribed shape – here a constructive imagination, a sense for geometrical shapes and their properties can be well practiced; a child is sensing an area.

·       To fill in a bound area with parts – here there are three possibilities:

o       The shape is given by its boundary.

o       All points of the shape are in one colour – a full shape.

o       The shape is placed in a square net.

When modelling via a given prescribed shape, the pupils have to compare the boundaries of the shapes, then to choose a corresponding part of Tangram and to assign it suitably oriented into the created shape. The pupils are imagining geometrical shapes, their size and position in space, the same shape in different space positions, etc.

When filling a bound area with parts, there are different levels of difficulty. As investigations show, the pupils of lowest grades do not sense the square net as a tool which assists them in their work with rectangles, but sense it as a two-coloured environment, thus as a paper with figures. Their have to learn gradually “to sense” the parallels and the normal. They are most successful in their work if the given shape is given by its boundary.

In teaching geometry at lower secondary school, Tangram can be used in various motivating tasks, in practicing areas, perimeters, axis symmetry, and similarities of shapes, in proving the Pythagoras theorem and in exposition of rational numbers. It also contributes to practicing the isometric transformations in geometry. However, it is not an ideal tool for teaching the geometrical concepts as it consists of only one of seven types of triangles (the right-angled isosceles triangle), from two quadrangles (the square and the parallelogram) and it does not contain a circle.

the main idea

The influence of one-coloured and multicoloured educational aid on the work efficiency of pupils. Developing an ability to sense a boundary and area of a non-convex plane shape.

The influence of a graphical environment (square paper, coloured paper, plane-white paper) on the ability to project a given model into plane-drawing. Find out the perimeter and area of the different parts of the puzzle.

1.     Title: Tangram for measuring perimeter and area

2.     Mathematical topics for development:

Measuring planar shapes by using a non-standard measure unit

3.     Description of the activity

The general aim of this proposal is to make the teacher trainees think of the importance that problem activities of measuring can bring to the mathematical development of pupils. We use the game of Tangram in seminars for the teacher trainees in their preparation for teaching geometry to pupils aged 11–14 (that is, at lower secondary school). The main goal is the development of creative thinking and geometric imagination of pupils. We also aim at preparing a school activity in which we deal with the concepts of perimeter and area in different contexts. We want to use Tangram to demonstrate isometric transformations in measuring perimeter and area.

We focus on the following partial aims:

·       Didactic clarification of the sequence of steps in modelling the geometrical terms of perimeter and area of planar shapes: perception – modelling – drawing in the plane – measuring – derivation of functional relations.

·       Describing van Hiele[1] levels of geometrical thinking, in particular with focus on deduction of functional relations using geometric terms.

·       Modelling the world of numbers and shapes using a line segment as a unit.

·       Finding relations between perimeter and area of different shapes.

·       For 14 year pupils only: measuring the sizes of different shapes and calculating their perimeter and area by using also Pythagoras theorem or algebraic expressions.

4.     Aims

For pupils

·       Combining the use of arithmetic, algebra and geometry within given activities.

·       Using Tangram puzzles for modelling and measuring perimeter and area in plane geometry.

·       Making conjectures, taking decisions, checking and verifying the results.

For teacher trainees

·       In Mathematics: To study different problems of measuring in geometry (to model relations between numbers and shapes).

·       In Methodology: Working in groups – development of didactic material to enhance pupils’ motivation. Testing of the materials carried out in 4 steps:

o       perception, modelling and drawing

o       definition of concepts and measuring

o       procedure for composition

o       decomposition.

For trainers

·       Guiding the trainees to adapt the lesson plan and teaching materials to the pupils’ age, level, individual needs and responsibility for selection of tasks, etc.

·       Providing instructions and feedback.

5.     Assignments

For teacher trainees

Perception, modelling and drawing

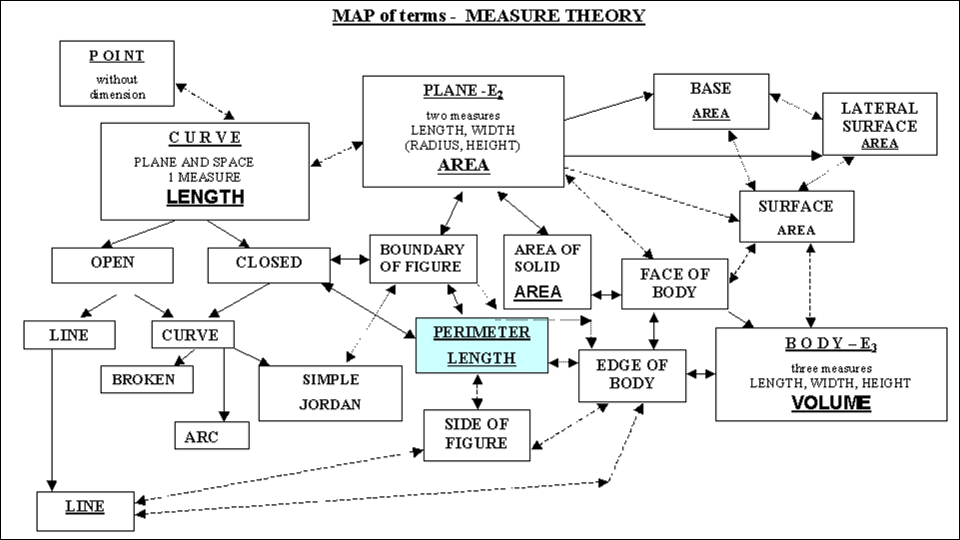
Task no 1 – The teacher trainees become familiar with the rules of the game Tangram. They draw pieces of the game according to Figure 1 on a paper. The teacher trainees prepare the game in two versions, plain and coloured, meaning that for the plain version they leave the geometrical shapes 1–7 blank and for the colour version they use different colours for the neighbouring shapes. They cut the pieces of the Tangram in both versions. The teacher trainees use the pieces of the Tangram in both versions separately to model the different Puzzle pictures in Picture 2.

The teacher trainees use all the parts of the Tangram to create the different shapes in Figure 2 as well as other shapes, for example, a girl, a candle, etc.

They copy (draw by hand) each of the created models in both versions (plain vs. coloured) on three different sheets of paper: blank, squared and coloured.

The teacher trainees discuss the influences of the different background environments on the sheets of papers as well as different Tangram versions on the ability to copy the exact shape of the Puzzle pictures created by Tangrams.

Afterwards the teacher trainees discuss the influence of the different coloured pieces on the ability to perceive the outline of the shape. They should also note the different influence of the Tangram versions (plain vs. coloured) on seeing the boundary lines of the drawn pictures.

In the next step the teacher trainees discuss the potential of the Tangram game on teaching the classification of quadrangles to pupils aged 11–14.

 

Picture 2. Puzzle pictures

Definition of concepts and measuring

Task no. 2 – (See also the Map of Terms or the Slovak website) The teacher trainees find the meaning of the concepts perimeter and area in different contexts in a thesaurus. They investigate the concepts perimeter and area in different contexts (geography, literature, electrotechnics, civics, arts, geometry…). By this activity we want to emphasize that the perimeter (the area) is in mathematics understood as length of a closed curve given by the (ordered) pair [number; measure] and not as a boundary (area) of a planar shape.

Procedure of composition

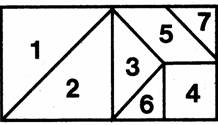
We can use two units – one unit is the side of the square 4 (call it s), the other unit is the hypotenuse of the triangle 7 (call it h).

We show that, given a perimeter (area), one can make, according to the instructions, planar shapes with different area (perimeter).

Task no. 3 – From two congruent triangles of Tangram (i.e. from either 1 and 2, or 6 and 7), model planar shapes so that you identify the sides of the same length. Draw the modelled solutions in your exercise book. Express the perimeter of the modelled shapes using the length units s and h. Video 1

Task no.4. – From the square 4 and the two triangles 6 and 7 of a Tangram, make planar shapes so that you identify the sides of the same length. Find all solutions and classify them according to the perimeter, according to the number and the size of the angles and according to the parallel sides.

By fitting the shapes together, pupils can see that one side of the triangle is longer than the side of the square. So, there are possibilities for an interesting and didactically fruitful discussion – what do we do about this? Suppose we are not allowed to measure – how do we classify the shapes? Which shapes have the same perimeter?

We can use two units – s and h. So, the perimeters are: A is 6s, B is 4s + 2h, C is 4s + 2h, … etc. (In fact, you can see that they are all 4s+2h, except shape A.) This motivates the use of symbols (s, h) to solve a problem and also leads to the question

What are the perimeters of all the other Tangram shapes?

Picture 3. Results

Decomposition procedure

Task no.5 – Students put together all parts of the Tangram and create: a) triangle, b) square, c) rectangle. Watch carefully and find differences between plain and coloured puzzles.

Task no.6 – Create triangles from 2, 3, 4, 5, 6 and all parts of the coloured Tangram. Draw the colour models. Find all solutions consisting of five parts.

Task no.7 – A little girl Barbara created a five-sided figure. Look at the Picture 4 and form a new one from the parts numbered 3 and 5. What other parts of the Tangram do you need to create the same shape? One of the solutions is to use the parts 4, 6, 7. Find all other solutions.

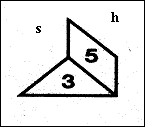
Picture 4. A five-sided figure

Area and perimeter of planar shapes

Task no.8 – Create all possible shapes from the triangles 6 and 7. If the unit for the Tangram pieces is the length side of the square s and the hypotenuse of the triangles is h, study the relations between the perimeter and area.

You do not have to know of height triangles nor do you need to measure the area in order to classify the shapes. We can use one unit of area – T (the area of the triangle 6 or 7). All shapes have the same area – 2T.

Task no.9 – Create the shapes in Figure no.3 from the triangles 6 and 7 and the square 4 of the Tangram. Compare the perimeters and the areas of them.

Task no.10 – If the unit of the area is the one of the smallest triangle of the Tangram – T, find the areas of the different parts of the puzzle.

Special Task

A boy John put the middle triangle numbered 3 on the top of the large triangle of Tangram numbered 1 as seen in Figure no. 4. Calculate the area of the newly created trapezoid (coloured in blue) using the units s and h (should it be the same as the area of the triangle 3?) Express that area in cm²: the length of the small side of the triangle no. 1 is 6 cm and the length of the hypotenuse is 6√2 cm.

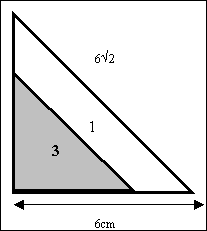
Picture 5. Triangle

For pupils

The pupils draw pieces of the game according to Picture 1 on a paper. They prepare the game in two versions, plain and coloured, meaning that for the plain version they leave the geometrical shapes 1–7 blank and for the colour version they use different colours for the neighbouring shapes. They cut the pieces of Tangram in both versions. The pupils use the pieces of the Tangram in both versions (plain and coloured) separately to model the different Puzzle pictures in Picture 2 and to become familiar with the rules of the Tangram game.

They copy (draw by hand) each of the created models in both versions (plain and coloured) on three different sheets of paper: blank, squared and coloured. Afterwards the pupils discuss the influences of the different background environments on the sheets of papers as well as different Tangram versions on the ability to copy the exact shape of the Puzzle pictures created by Tangram.

The pupils discuss the influence of the different background environments of the drawn pictures on the ability to see their boundary lines. They should also note the different influence of the Tangram version (plain vs. coloured) on seeing the boundary lines of the drawn pictures.

In the next step the pupils create a cat, a dog, a hare using all parts of the Tangram and discuss the potential of the Tangram game on teaching the classification of quadrangles. Video 2

They learn the mathematical concepts in English: base, height, hypotenuse, right angle, perpendicular and (in the case of the Tangram) isosceles, and the notions related to symmetries like transformation, rotation and translation.

They explain the terms perimeter and area in different contexts.

They can use two units – one unit is the side of the square 4 (call it s), the other unit is the hypotenuse of the triangle 7 (call it h). They find out that, given a perimeter (area), one can model, according to the instructions, planar shapes with different area (perimeter).

The pupils create models from the Tasks no. 3 and 4. Create all the shapes you can by putting congruent sides together. They discuss in groups how many solutions are there to this problem.

If the unit of the area is the smallest triangle of the Tangram – T, find out the area of the different parts of the puzzle.

Making conjectures, taking decisions, checking and verifying the results.

Bonuses in individual work for best pupils are the tasks no. 6, 7 and special.

For the trainers

·       Guiding the trainees to adapt the lesson plan and teaching materials to the pupils’ age, level, individual needs, responsibility for selection of tasks, etc.

·       Providing instruction and feedback

Conclusion

This proposal is designed for teacher trainees of Mathematics in 6-9^th grades at basic school (age 11-15) or in early grades of the grammar school and also as a compulsory part of the course in Didactics of Mathematics.

The venue: Pedagogical Faculty, Matej Bel University, Banská Bystrica.

The trainers: Teaching team created by university lecturers, 1 trainer and 2 teachers of Mathematics and 1 of English.

Trainees: 18 prospective teachers in the course Didactics of Mathematics.

 

The time schedule – 2 lessons per week

 

Table 1. Time schedule

Realisation of proposal sequences

Realisation in the classroom

Evangelical Gymnasium Banská Bystrica, Skuteckého 5. It comprises 8 grades of lower and upper secondary school, class quarts, age of pupils 12/13, number of pupils 21. Mathematics in English, Geometry in English. Two teachers – English and Mathematics.

Teachers taught alternately. Student of course recorded a video.

Primary School Amos in Martin, Východná, class 5^th, alternating teaching of Maths and Science. Number of pupils 23. Two teachers – teacher and trainee. One teacher taught. The teacher trainees recorded a video.

The classroom

Modelling in plane (E₂) – Teacher motivates the pupils.

Classification of quadrangles.

Composition and decomposition procedures.

Perimeter and area.

Suggested reading

Brincková, J. (1996) Didaktická hra v geometrii (Didactical games in geometry). Bratislava: DONY

Brincková, J. (2001) Tvorivé dielne 2 (Zamerané na didaktické hry). Banská Bystrica: PFUMB

Millington, J.: Tangram. Puzzle picture to make you think!

 

 

Picture 6. Measure theory

 

 

Trainees have to arrange as many different plane drawings or plane geometrical figures as they can, by using a classical 7-pieces Tangram (eventually built up by themselves). Then they will have to look at geometrical properties (convexity, number of vertices…) of such different shapes, in order to discover general relations or to give a classification of them. In particular they are asked to use only some designated pieces, while trying to construct regular polygons. Area and perimeter properties of the (non congruent) figures so built have to be also considered.

Similar activities will be performed with pupils and the results of their piloting will be afterwards discussed with trainees.

Mathematical topics

The proposal is related to geometrical properties of drawings, in particular to the measures of area and perimeter and to isometric transformations.

Aims

For trainers

·       Guiding trainees from theory to practice.

·       Letting the trainees experience an activity on their own, before proposing it to the pupils.

·       Providing instructions and feedback.

For trainees

·       Discussing about basic notions of geometry and how to present them.

·       Realizing the difficulty of defining and naming a “geometrical figure”.

·       Experiencing a classification activity on non standard figures.

For secondary school pupils

·       Knowing basic names and notions about some common polygons.

·       Being able to measure the length of a segment (directly or, if necessary, by means of Pythagoras’ Theorem).

·       Realizing the equivalence of plane figures which can be decomposed into the same parts.

·       Working on plane figures by means of isometric transformations and their compositions, realizing that new figures are congruent to the previous ones.

Description of the activity

Activities took place in SSIS School and involved 42 students, both first and second year, of SSIS, specialisation Natural Sciences, for the qualification to teach Mathematics and Science in lower secondary school.

Phases and timing

·       Presentation of Tangram and activities about geometrical figures (1h30’) Video 1

·       Discussion and design of a proposal to be carried out in class (45’)

·       Piloting in the classroom (between 3 and 5 hours, depending on the classes)

·       Final discussion (30’)

SSIS students were given cardboard copies of a Tangram to be cut out. The three following activities were proposed and then commented upon jointly:

·       To make up an 8 by 8 squares grid on which to report coordinates of vertices that had to be joined to form the sides of the figures that constituted the Tangram puzzle: (8,0) and (0,8); (0,0) and (4,4); (8,4) and (4,8); (2,6) and (4,8); (6,2) and (6,6); (4,4) and (6,6).

·       To form all possible geometrical shapes using the square and the two small triangles and putting congruent sides aside. The obtained figures had to be classified according to the number of vertices, area and perimeter. Video 2

·       To use all Tangram pieces to construct a known polygon: triangle, square, rectangle. Video 3

In the discussion that followed the activities, students were invited to answer the following questions, mainly focusing on the didactical aspects of the activity:

·       Which competencies are involved in this type of activities? Which pre-requisites are needed? What type of learning is promoted?

·       What difficulties did you meet in this activity? Do you think pupils would meet further difficulties? How can they be helped overcome them?

·       How might we outline a classroom activity with this instrument? At what teaching level? Which are the most important points to focus on, in your opinion?

Later, two trainees who were already teaching carried out a classroom teaching experiment: the choice was due to the fact that they could work in known classes and include the activity in the classroom standard syllabus. The proposal, mainly sketched during the preliminary discussion, was taken by trainees and adapted to their own teaching context; experimentation took place in four classes (totally about 80 pupils aged between 11 and 14); one of these two classes used it as a peer tutoring activity with primary school classes.

Pupils were given a classic square Tangram made of 7 pieces (either to cut out or to construct on a coordinates grid). They were invited to construct different plane figures (either fancy or geometrical ones) by using these pieces, and then make hypotheses and verify conjectures about them. In particular they were invited to construct figures with some given pieces (in some cases all of them), identifying which figures are congruent, making conjectures about possible classifications and reflecting upon both extension and perimeter of the figures constructed in this way.

At the end, experimenters reported on their activity to others, making comments on the hypotheses emerged from the preliminary discussion. Finally the whole group proposed some particularly meaningful activities for further analysis.

PRESENTATION

Geometry learning, especially in primary and lower secondary school, is particularly important, beyond the mere set of learned notions related to a specific theme.

Geometry plays a crucial role in the formation of rational thinking both as spatial organizer and as providing a rational description of space.

“Geometrizing” our experience of the world around us is a primary mathematical activity, preceding the very counting activity. Children mainly and spontaneously tend to represent their experiences through graphical-pictorial activities, before enumerating objects around them. This graphical-pictorial activity tends to both represent and interpret our experience of reality; it is mathematics that at some point, offers specific instruments to describe these real objects: lines, points, figures…

Geometry thus originates from observation, manipulation, construction and representation of simple objects, from folding, cutting, putting together, from looking at both oneself and everything around in the mirror… The subsequent “geometrization” is neither easy nor simple, it requires a capacity of “interpretation” that allows for detachment from a naive view to get to a complex rational understanding. Geometrical thinking shapes up throughout the whole school life span through the different teaching and learning levels, merging together concrete and rational aspects of geometry, even though the former or the latter prevail in different moments of the school experience.

In order to exemplify this point let us consider “geometrical figures”. The first approach is to operate on (elementary and regular) geometrical figures, describing their shape and properties: this can be defined the “visual” level. This approach normally characterises the first years of primary school (6 to 8 years old pupils). Later we move to recognizing and describing figures on the basis of learned properties, at a “descriptive analytical” level. Then pupils construct definitions, look for characterising properties and need to argue and prove: this is the highest and most abstract level, leading to the “formal” one envisaging proof of theorems and study of geometry axiomatic system (or rather axiomatic systems).

Being able to operate with figures and drawing them become important instruments for geometry learning: drawing figures one is able to visualise features and properties, because properties of a geometrical object are translated graphically by means of spatial relationships. However, the inverse path, leading from the drawing to the geometrical object, comes from a human subject’s interpretation act: recognising visual spatial properties attached to geometrical properties is not a spontaneous activity and thus needs a proper learning process. A (geometrical) drawing can be interpreted in many ways in different contexts and perception comes in when an interpretation is constructed: this might be incorrect, especially when the reader’s theoretical notions are limited and do not allow him/her to go beyond a perceptive reading.

Moving from the object to the geometrical drawing by identifying features and from the drawing to the geometrical object by means of interpretations show how graphical activity and its gradual refinement are both consequence and source of learning. For instance through them it is possible to highlight contradictions in theoretical misconceptions (it is extremely difficult to make the “heights” of a triangle that follows the squares borders meet exactly …) or advantages of a theory that permits us to “predict” general consequences (equality of the third sides of two triangles having two sides and the angle between them respectively equal…).

Highly relevant within this conception of geometry learning are those activities that are posed as borderline experiences, presenting both playful and graphical aspects and at the same time, offering opportunities for an abstract mathematisation. Too often does the teaching practice skip these transitional moments and the most delicate time is exactly the beginning of lower secondary school when insistence on definitions and formulae detached from a concrete context contributes to a (often definitive) distortion of the view of mathematics. Geometrical aspect is seen and perceived as defined by the mnemonic knowledge of definitions and formulae. Therefore it seems necessary to put enough care to the description and evaluation of this type of activity in teacher training.

The proposal about the use of Tangram we piloted lies on this educational line.

ACTIVITIES WITH TRAINEES

All SSIS students were given a copy of a Tangram puzzle on an easy-to-cut-out sheet[2].

In the introductory part of the experience we detached from the scheme proposed by Slovak colleagues: due to time limitations we avoided that SSIS students worked on the construction of free figures with Tangram. Trainees were anyway made aware that in this activity, as well as in any other manipulative or laboratory-like activity, the initial phase should involve free exploration; hence the need to leave pupils some time to “play”, to explore the different pieces available and try to use them for various creative productions.

We then started a path with SSIS students by presenting on transparencies a Tangram puzzle and a set of figures that could be made with it. It was pointed out that it would be desirable that pupils be encouraged to work either individually or in small groups to construct these images or invent new ones. This phase might initially seem to be useless from a mathematical viewpoint (many trainees shared this opinion, although they later changed their mind) but it is crucial on the motivational plane and for allowing pupils to make contact with the material and explore intuitively its limits and potentials.

Looking at the slides SSIS students were asked whether they considered the activity easy for their students and how they could think about a mathematical educational aspect of this phase of the activity (always keeping in mind the playful and motivational aspects). In the discussion that followed there were few and all agreeing interventions: the activity was easy, relevant to interdisciplinary links (with Arts and Technical Education) but scarcely meaningful from a mathematical viewpoint. We believe that this perplexity shows the distorted view of the discipline we referred to earlier: despite previous laboratory-like experiences, trainees hardly see the potential geometrical learning in activities where an informal approach prevails[3].

It is interesting to show that later, in the classroom activity, this phase was dealt with before the actual geometrical work. In the final discussion they remarked that pupils found the activity relatively easy and could realize the proposed figures smoothly. However trainees themselves pointed out how this activity contributed to highlighting a series of “properties” of figures that teachers tends to take for granted, especially those properties that relate to the dynamic nature of the position figures take up in the plane (it is known that many pupils tend to visualise geometrical figures in a static way), or to the different configurations of the borderline between Tangram shapes, that come to constitute the different regions of the composed figure: this borderline may be a point or a segment, may include part or the whole side of an elementary shape etc. Working in class on finding a linguistic definition of these situations led to an enrichment in the geometric vocabulary and served as a basis for next phase. In the light of this remark it might be not useful to include this phase also in the SSIS training activities.

Activity 1 of course requires notions about the Cartesian plane (together with precision and manual ability). Trainees met no particular difficulties with it but they supposed their pupils would meet some, since they did not have all the needed pre-requisites about the Cartesian plane. In case these pre-requisites were held by pupils, trainees proposed that pupils might be showed the Tangram shape and then provided with only some of the coordinates. In the discussion it was pointed out that, due to symmetry reasons and to the size 8=2³ of the chosen grid, all vertices of the Tangram portions on the grid have anyway integer coordinates, although many segments have irrational length. From the didactical viewpoint it was interesting to notice that different competencies are required to join points with given coordinates or to indicate coordinates of points in the plane: in this way it is possible to construct different requests, suitable to re-enforce or promote different competencies depending on the pupil’s needs.

Activity 2 presented to trainees two different types of difficulties (surprising for students themselves…): the need to identify and define a mechanism for classification that identifies two congruent figures and the impossibility of “naming” all the figures. This latter point in particular highlighted the belief that geometrizing is too often synonymous with “naming”. Certainly the activity was useful for pre-service teacher training, because, once in the classroom, they could manage pupils’ “discovery” of non standard polygons with greater ease. Students also pointed out the relevance for teaching of this proposal in order to promote creative competencies in pupils, who are invited to experience a form of autonomous mathematical classification. However we decided to present the activity as group activity, since requested competencies are possibly not available to every single pupil at the age we considered: group activity will permit exchanges with all the possible advantages coming from this.

A reflection that came out immediately with trainees, but that might not be as such for pupils (and in fact it was not) is that it is not possible to classify by the area of figures constructed with the same pieces, given that these figures are equivalent, being all equally decomposable.

Difficulties met in activity 3 may be mainly reduced to difficulties (well-known in gestalt psychology) in de-structuring and re-structuring one’s vision, so as to visualise the given figure as part of another one, whose structure in mind is again strong and rigid. We notice here that in classroom activities pupils were much faster and capable in carrying out these activities, possibly due to a less rigid structure of the geometrical figures they held. This was predicted by most SSIS students, who had supposed that pupils could be more capable because of an envisaged higher visual capacity.

CLASSROOM EXPERIMENTATIONS

Four of the SSIS students volunteered to present the activity in their classes. The scheme of the proposal was agreed during a collective discussion, adapting it to the different classes and to the topics of the syllabus they were working on. Trainees involved in the experimentation (the class teacher and another trainee) were asked to pay attention to the points highlighted in the discussion, also to test the hypotheses made about difficulties and meaningfulness of the activity.

A point shared by all experimentations was (also due to the fact that activities were carried out in February) that all the involved classes counted few pupils because of flu or winter extra-school activities.

The following are excerpts from trainees’ final reports

Grade 6, 5 hours work, 12 pupils involved

[Tangram was made starting from the coordinate grid, the construction of which allowed for a revision of notions about the Cartesian plane. After that the teacher left pupils free to play with pieces]. As soon as they cut out the seven pieces they starter to compose them, turn then around, put them together to obtain images in such an enthusiastic way I did not really anticipate. The most amazing comment was “This is real mathematics!” which meant, as its author later explained, that “we are having fun and thinking a lot and racking our brains at the same time”.

Then I proposed that rules were fixed to hold for everyone: we had not to overlap pieces, put them aside by the sides, always use ALL the pieces. After an initial moment of doubt, pieces started to turn around every desk. A moment of glory was reserved to the Chinese girl who joined the class two weeks ago, without knowing any Italian, who, after copying and cutting the scheme in silence started to compose more and more complicated figures, laughing: the first woman, the first boat … I could not and neither wanted to interrupt them until a boy constructed “a trapezium, mister, a trapezium!”. I took the opportunity: “Oh, yes, and it seems to me that we can construct also squares, triangles, rectangles …”. It was a new challenge: always with all seven pieces. Almost all pupils engaged in the search and the rectangle that we, as SSIS students found in 5 to 6 minutes came out in less than a minute and a half. I checked discretely and invited the girl who made it to cover it, because I wanted to see what the others were doing: well, in less than 5 minutes every single student had their own rectangle constructed.

Starting from there I asked them to observe and reflect on the extension of each figure, and starting from figures that occupy the same surface we moved to think about them as made of the same pieces, which, although being moved around staying the same, give rise to different figures that nevertheless occupy the same surface. […] Pupils like this part very much because anyone could manipulate and compare pieces as they liked, get it wrong and try again. Other reflections came up when they had to observe the figures boundaries, after putting them on squared paper to measure their perimeter: how come we get the same area but so much different boundaries in some figures and not in others …?

Grade 6, 4 hours work, 16 pupils involved

I actually had observed in the past that pupils often meet difficulties in imagining geometrical figures beyond the book-workbook-geometry lesson context. In some cases I happened to have to guide them to recognise figures they had already drawn in the Technical education class and they only had to reproduce for the geometry class.

The class in which the activity was carried out is mainly composed by pupils coming from the same primary school class, who had already worked with Tangram, as I came to know at the beginning of the lesson. I thought it would be better not to make pupils work in the same way they used in primary school, so we moved to the computer laboratory where we connected to a web site which presents a game enabling pupils to play with Tangram’s seven pieces to re-create either fancy or geometrical equally extended figures. Pieces can be rotated (by 45° each time) translated or, only in the case of parallelogram, overturned.

The activity was fun for everybody and raised interesting remarks, such as for example:

   “it is weird for geometrical figures to turn around”

   “[parallelogram] fits in if I turn it upside down, it is as if it changed shape”.

In general it seemed to me that they were all engaged and we progressively commented that all the figures were obtained starting from the same modules by means of translations, rotations, flipping over without deformation. Also an autistic grade 8 pupil of mine took part in the activity and she amazingly could carry out correctly and quickly most of the game.

Grade 7, 5 hours, 15 pupils involved

Posed questions were understood by everybody. Also those who meet more difficulties in the class work participated autonomously and often found correct solutions.

In the first lesson pupils were invited to use the two equal isosceles triangles, putting the congruent sides aside to get the greatest possible number of different shapes […] I asked them to reflect on how to check whether figures were isoperimetric or not. The class thought they could use a ruler to measure the sides’ length, but when they found out that some dimensions were expressed in decimals, they decided to assume an arbitrary value as unit of measure, i.e. they assigned the smallest dimension the unitary value (we talked about it together) and by using Pythagoras’ theorem they found the other lengths.

I then asked whether the figures were equivalent. Only 10% of pupils answered correctly, so I needed to revise what I had done previously, suggesting they could work measuring the number of (paper) squares. The following week we used a square and a triangle, following the same method used in the previous class. This time the 85% answered correctly the question whether obtained figures were equivalent and isoperimetric.

After two days I asked them to form a rectangle, using all the Tangram pieces. After an initial critical moment they found 2 or 3 ways of getting it. I asked if the rectangle and square they had got from the pieces were equivalent and isoperimetric. In this case, they all answered correctly.

In general, regardless of the number of correct or wrong answers, I noticed that due to what they discovered in this activity pupils were led to reflect more before expressing the position. We got many solutions, although they were not extremely different. It is interesting that nobody thought about copying from their deskmate, as if the object under consideration were something personal. They certainly collaborated, but in a functional way to their solution needs. In particular a very good pupil (female) could not solve the problem [to find the area of one of the obtained figures] because she could not think using pieces. Some days later she confessed to me that when she solves a geometrical problem she only draws the figure to make me happy. Another girl, rather low-achieving, quickly solved the problem flipping a triangle (that she named figure 1) over the parallelogram (figure 2) writing down A₂ = 2A₁.

Grade 7, 4 hours for the initial phase + other 4 for tutoring, 14 pupils involved

[The initial phase was very similar to that carried out in grade 6 classes, also due to a certain general weakness of the class, which was involved in an activity of peer tutoring with pupils from a grade 3 primary school class (aged 8). The teacher thought she could use this tutoring to stimulate pupils to re-elaborate on their notions on a metacognitive level, in order to explain them to younger pupils.] The tutoring activity was proposed in two grade 3 classes and followed two distinct phases.

In the first phase, pupils, guided by older students, drew a 8 by 8 squares Tangram on squared paper with 1 cm side squares; the Tangram was then cut out and younger pupils invented and constructed different figures with the 7 pieces, giving each creation a “title”. At the end the children drew these figures on their workbooks.

The second phase envisaged an “enlargement” work, designed in collaboration with the Technical education teacher: “giant Tangrams” measuring 60x60 cm were constructed on 2.5 by 2.5 cm squared paper sheets. Tangrams were glued on cards and then cut out; each child was invited to recompose the figure already constructed and colour it as they fancied. The various pieces of each figure were fixed with adhesive tape, made stiff through bamboo sticks and then wore as masks.

At the end of the work there was a collective discussion in which younger pupils expressed their amazement in discovering that from initially identical Tangram they could make up such different figures. Older pupils tried to help the younger to understand why “some shapes look longer, even though they cannot have grown”, what changed from the beginning, when there was no difference between Tangrams. Among the sentences that most convinced young children we report the following, that seem to show an understanding of the work done and a non trivial capacity of verbal re-elaboration:

“Shapes are as big as earlier but the position of pieces changed”

“Parts without card changed, i.e. empty spaces” (of course behind this sentence hides the concept of equal extension, as it was clear to the boy who uttered it …).

COLLECTIVE DISCUSSION OF FEEDBACK

After trainees who experimented the activities in the classroom presented their reports, discussion focused on the motivational value of the activity (and everybody agreed on that), in particular on its potential to involve also pupils with scarce interest or capacity in mathematics. Much more interesting were pupils of different school level’s reactions: in the preliminary discussion some trainees had predicted that older students would have been less interested. This prediction was not confirmed, although it was noticed that younger pupils were actually more involved in the construction of fancy figures, whereas older pupils were soon ready to move to work on geometrical figures.

In this phase we also noticed how this work naturally stimulates the acquisition of techniques, methods and terminology linked to geometrical transformations. Hence the proposal was made to consider, in classes after grade 6, the activity as preparatory for a module of laboratory-like geometry, to be located after completing the polygon teaching unit and aiming to a reflection on equal extension and isometries (in particular symmetry, translation, rotation), as well as to reach competencies related to visualisation and recognition of geometrical figures in general.

PROPOSALS FOR FURTHER DEVELOPMENTS

At the end of the concluding discussion two further activities were proposed, one designed and partially already carried out by one of the trainees and the other presented by SSIS lecturers:

·       Tangram Web Quest. If you digit the word Tangram on any Internet search engine you get the list of a great quantity of web pages, many of them suggesting teaching activities. A suitable activity for trainees might be to identify the most significant activities for learning at their pupils’ school level; for pupils one might think about suggesting they connect to sites that contain a particular type of information or requests that enact further searches or readings.

·       Tri-dimensional puzzles. Some pupils, as well as adults, have strong capacities for spatial view and graphical representation; some others meet difficulties on this ground. And it is well known that these capacities are not necessarily at the same level as other mathematical abilities. There are students with high competencies on the verbal plane and for whom it is easier to memorize a sentence like “a solid with 8 vertices” rather than visualize its image; vice versa, one can perfectly visualize a cube and needing to count vertices and sides every time…. This difference in cognitive styles makes it necessary to propose to all students activities involving spatial view and verbal description of solids, so that students can complement their competencies and also weaker students on the computational and algebraic planes, but strong in this other field can perform highly.

To exemplify the mechanism, the following questions were proposed to SSIS students:

A. – “Imagine a tetrahedron and write down how many faces, sides and vertices it has. Imagine you open up the tetrahedron so that you get its plane unfolding. What is its shape? Is there only one?

A boy constructed a figure using squares and equilateral triangles, we do not know how many. We know that this figure has 5 faces, 5 vertices and 8 sides. What figure is it?”

The question was not given with drawings, but it left everything to the involved SSIS students’ spatial visualization.

SSIS students felt the need to clarify that a tetrahedron is a pyramid with triangular basis and four faces (“like the silicate ion of quartz” one of the trainee suggested, drawing on her degree in Chemistry) in order to be able to solve the first part of the question relatively easily; further steps to solve also other parts followed, with the support of hands for “constructing” the object in the air. Video 4

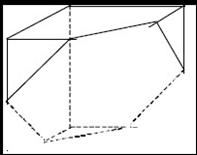
B. – “Imagine two different pyramids with squared basis, whose side faces are equilateral triangles. Put the two pyramids on a plane, getting them aside, so that they only share one (and only one) side of the basis. There is an empty space between these two solids. Would you be able to describe the solid that can fill in that emptiness, so that a convex solid can be obtained?”

Picture 7. Two 3D pyramids

C. – “Take 3 squares 10 by 10 cm, on one side of each of them cut out a right triangle with side 5. Consider also a regular hexagon with side 5Ö2. Combine now these 7 pieces to construct a solid as the one shown in Picture 8. Putting two of these solids aside what regular solid do we get?”

Picture 8. Our solid figure with 7 faces

The answers to questions B. and C. (respectively, a tetrahedron and a cube) is not intuitive and this type of exercises exemplifies to trainees those difficulties in spatial visualization we referred to earlier; at the same time, both among trainees and in the classes where the activity was implemented, some manage to “see” the solution much earlier than others (sometimes surprisingly) and immediately become tutors and leaders for classmates.

D. – “Take simple cubes (like wooden blocks) and try to construct a solid with a fixed number of these cubes. Represent then this solid from the different possible perspectives (frontally, from the right side, from the left side, from the top) using a given dotted grid. Conversely, given its representations, reconstruct the solid.” Video 5

Of course in this type of activity, the main difficulty lies in having representations on different planes, some of which hidden to sight, and thus requiring a great effort for spatial representation. However this activity is also suitable for creating links to other disciplines like Technical education and Arts, beyond offering a good support to a rational description of what is actually achieved each time.

SUGGESTED READING

Gardner, M. (1956). Mathematics, Magic and Mistery. Dover Pub.

Kanizsa, G. (1973). Il ‘problem-solving’ nella psicologia della gestalt, in Mosconi, G. e D'Urso, V., La soluzione dei problemi. Firenze: Giunti-Barbera.

Jaglom, I.M. (1972). Le isometrie. Bologna: Zanichelli.

Pellegrino, C. (1999). Prospettiva: Il punto di vista della Geometria. Bologna: Pitagora Ed.

UMI-CIIM (2001). Matematica 2001, Materiali per il XXVII Convegno Nazionale sull’Insegnamento della matematica. Lucca: Liceo Scientifico “A. Vallisneri”.

 

 

The general aim of the proposal Tangram piloted in Slovakia was to make the teacher trainees think of the importance that problem activities of measuring can bring into the mathematics formation of the pupils. We used the game of Tangram in seminars for the teacher trainees in their preparation for teaching static and metric geometry to pupils aged 11–14, that is, at lower secondary school. The main goal was the development of creative thinking and geometric imagination of pupils via using Tangram at school. We aimed at preparing a school activity in which we could deal with the concepts of perimeter and area in different contexts. We wanted to use Tangram to demonstrate isometric transformations in measuring perimeter and area, too.

We focused on the following partial aims:

·       Didactic clarification of the sequence of steps in modelling the geometrical terms of perimeter and area of planar shapes: perception – modelling – drawing in the plane – measuring – derivation of functional relations.

·       Describing van Hiele levels of geometrical thinking, in particular with focus on deduction of functional relations using geometric terms.

·       Modelling world of numbers and shapes using the term measure of abscissa.

·       Finding relations between perimeter and area of different shapes.

Partners in Florence (Italy), who co-piloted the project Tangram, provided us with the following feedback (their view of the project):

The proposal is related to geometrical properties of drawings, in particular to the measures of area and perimeter and to isometric transformations. It is planned as a laboratory activity, so that pupils have to use their perceptive, manual and logical skills, starting from concrete objects to achieve geometrical and graphical competences. Pupils, at the end of activity, are expected

·            to know basic names and notions about some common polygons

·            to measure the length of a segment (directly or, if necessary, by means of Pythagoras Theorem)

·            to realize the equivalence of plane figures which can be decomposed into the same parts

·            to work on plane figures by means of isometric transformations and their compositions, realizing that new figures are congruent to the previous ones.

Our partners in the Czech Republic cooperated with another teacher training institution (South Bohemian University, České Budějovice, teacher trainer Helena Binterová) in order to co-pilot the Tangram project. They provided us with the following variation of project aims:

Make future elementary school teachers familiar with the didactic means “Tangram” so that they are able to use it later in their teaching, in lessons of plane and metric geometry. The main aim was to define concepts, to develop creative thinking and geometric imagination and to make the student teachers aware of related didactical difficulties.

One of the compulsory assignments for the teacher trainees was to prove Pythagoras’ theorem as well as sketch and justify the selected procedure.

The aims of all three participants of the project Tangram have been essentially identical. The pupils could develop their geometrical imagination via a didactical game and to strengthen their knowledge from isometric and metric geometry.

The teacher trainees prepared differentiated classes. They studied the problem of mapping in metric geometry via a priori analysis. They could see the theme of modelling in geometry from a new perspective via a posteriori analysis.

 

© LOSSTT-IN-MATH Project